前言
咱们搞3D开发,肯定是需要一定的数学知识的。本篇文章和大家一起来学习一下我们应该掌握的基础数学知识,大致分为3个模块
- 三角函数
- 向量
- 矩阵
本篇先来讲三角函数,先带大家回顾一下初中数学中的三角函数,就比如这样一个角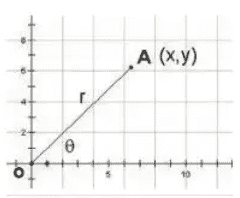
定义式
推导过程我就省略了,毕竟有点麻烦,直接给结果
正弦(sin)公式
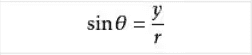
余弦(cos)公式
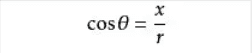
正切(tan或tg)公式
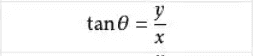
余切(cot或ctg)公式
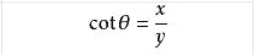
正割(sec)公式
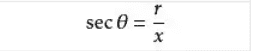
余割(csc)公式
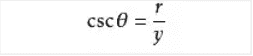
函数公式
倒数关系
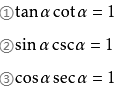
商数关系
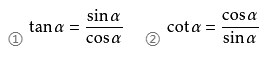
平方关系
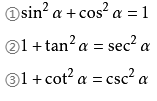
诱导公式
公式一
设α为任意角,终边相同的角的同一三角函数的值相等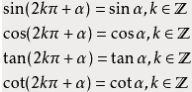
公式二
设α为任意角,α+π与α的三角函数值之间的关系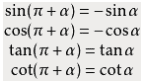
公式三
任意角-α与α的三角函数值之间的关系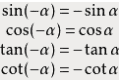
公式四
π-α与α的三角函数值之间的关系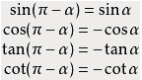
公式五
2π-α与α的三角函数值之间的关系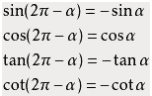
公式六
π/2 ± α 和 3π/2 ± α与α的三角函数值之间的关系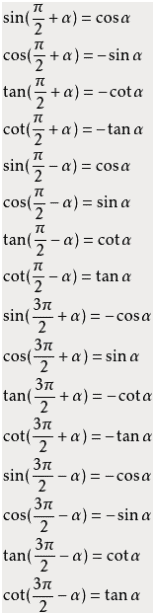
诱导公式总结
奇变偶不变,符号看象限
理解诱导公式总结
这句话怎么理解呢,其实很简单
先看第一句:奇变偶不变
就看那个π的参数是多少,我们都知道π是180度,那么π/2就是90度了,你就看他的系数是几个π/2,如果是奇数个,就需要变化函数了,按照以下的规则进行变化:
正弦(sin)变余弦(cos),余弦(cos)变正弦(sin),正切(tan)变余切(cot),余切(cot)变正切(tan)
如果是偶数个,那就不需要进行变化,比如π啊,2π之类的。
再看第二句话:符号看象限
我们都知道, α是一个锐角(假定的锐角),然后根据每一个弦在四个象限中值的正负关系进行逻辑判断
如下图所示:
我们将象限定义为以下4个,分别为第一,第二,第三,第四象限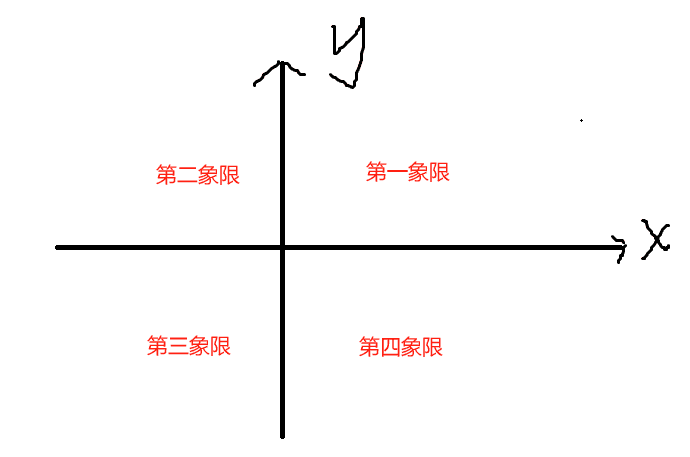
此时比如我们以sin进行举例,我们都知道sin的公式是y/r,已知r的长度肯定是正的,那么y就决定了他是y/r的正负关系了
如此看来,在sin函数中,第一第二象限的角是正的,第三第四象限的角是负的。
同理可以推的cos的公式是x/r,那么第一第四象限的角是正的,第二第三象限的角是负的。
其他的大家可以根据定义式自己去推算以下,这里我就不多阐述了。
然后我们知道某个函数在某个象限中的正负关系了,就可以使用符号看象限的公式了
总结方法使用举例
sin (π/2 + α) 等于什么呢?
首先π/2的参数有一个π/2,是一个奇数,所以根据奇变偶不变,我们可以得到他是要变成cos的,然后根据符号看象限,
90度+一个锐角α,很明显是在第二象限的角度,此时sin是正的,所以sin(π/2 + α)=cos αcos (13π/2 - α) 等于什么呢?
首先我们要明白一个道理,一圈是2π,所以当我们的系数远大于2π的时候,我们可以先把它给约掉,比如13π/2里面有5个2π,可以先约掉,此时我们的cos (13π/2 - α) = cos (3π/2 - α),然后我们可以根据奇变偶不变,可以得到有3个π/2,是一个奇数,那么他是要变成sin的,然后根据符号看象限,3π/2 - α的角是一个在第三象限的角度的,此时的cos是一个负值,那么就得到了cos (13π/2 - α) = -sin α
结语
本篇文章就先到这里了,后续我会带来学习3D所需数学知识的向量和矩阵部分,敬请期待,债见~