前言

有小伙伴和我说前几篇的从入门到放弃WebGL里面的那些个类和一些方法不太看得懂，那我依次一个个来推导说一下。

方法:getMousePosInWebgl

用处

将 CSS 的位置变成 Webgl 的位置

代码

function getMousePosInWebgl({ clientX, clientY }, canvas) {
  //鼠标在画布中的css位置
  const { left, top, width, height } = canvas.getBoundingClientRect();
  // 当前点击的点在cavans中的坐标
  const [cssX, cssY] = [clientX - left, clientY - top];
  //解决坐标原点位置的差异
  const [halfWidth, halfHeight] = [width / 2, height / 2];
  const [xBaseCenter, yBaseCenter] = [cssX - halfWidth, cssY - halfHeight];
  // 解决y 方向的差异
  const yBaseCenterTop = -yBaseCenter;
  //解决坐标基底的差异(因为webgl中，他是（-1，1）的，而不是（-width/2,-height/2）,所以要除以`halfWidth`和`halfHeight`)
  return {
    x: xBaseCenter / halfWidth,
    y: yBaseCenterTop / halfHeight,
  };
}

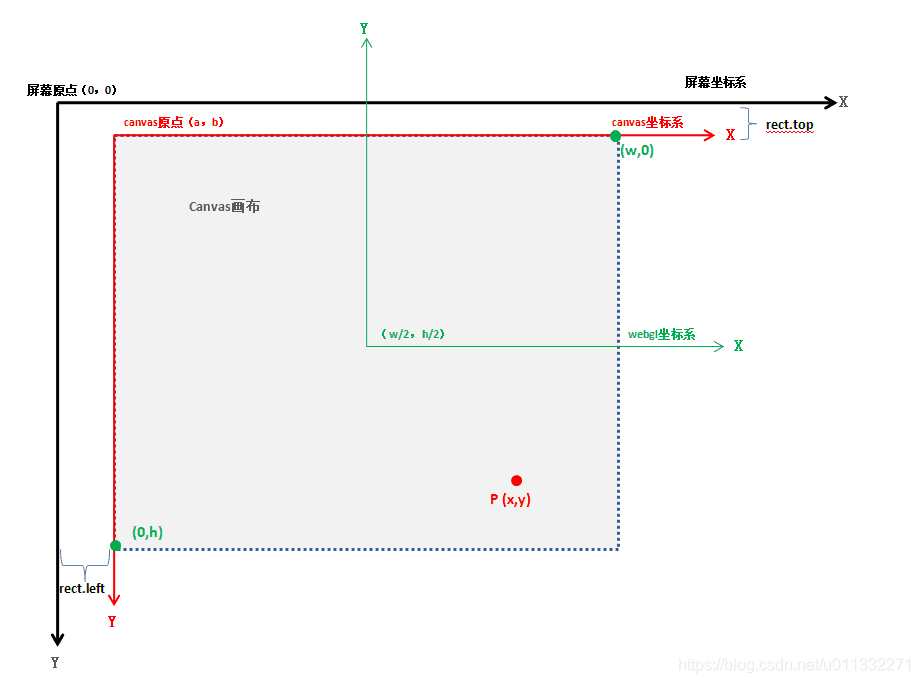
方法:glToCssPos

用处

根据 webgl 坐标得到 canvas 坐标原点移动到 webgl 中的原点的位置的坐标

代码

function glToCssPos({ x, y }, { width, height }) {
  const [halfWidth, halfHeight] = [width / 2, height / 2];
  return {
    x: x * halfWidth,
    y: -y * halfHeight,
  };
}

这里很好理解，就是把上面的getMousePosInWebgl去掉了最后一步的基底转化和方向变化，得到的 x,y 就是getMousePosInWebgl中的xBaseCenter, yBaseCenter,即将 canvas 坐标系的原点移动到 webgl 坐标系原点的位置的坐标

方法:ScaleLinear

用处

得到两点之间的直线关系公式（点斜式），这个直线上的所有点都满足这个点斜式关系

代码

//线性比例尺
function ScaleLinear(ax, ay, bx, by) {
  const delta = {
    x: bx - ax,
    y: by - ay,
  };
  const k = delta.y / delta.x;
  const b = ay - ax * k;
  return function (x) {
    return k * x + b;
  };
}

我们都知道，两个点，可以构成一个点斜式关系，就是 y=kx+b;假如我们有两个点（ax,ay）,（bx,by）,那么斜率 k 就是(by-ay)/(bx-ax),此时的 b 就等于ay-ax*k或者by-bx*k,然后这个函数返回了k*x+b的关系式。

然后我们可以看到，我们在图形转面里面是这样使用的

1
2
3

//建立比例尺
const scaleX = ScaleLinear(0, minX, 600, maxX);
const scaleY = ScaleLinear(0, maxY, 600, minY);

也就是可以得到这个 x 和 y 分别的对应关系，这里的 maxY 和 minY 的位置互换是因为 webgl 坐标系坐标的 y 轴是向上的。

类:Compose

用处

承担容器的作用

代码

export default class Compose {
  constructor() {
    this.parent = null;
    this.children = new Set();
  }
  add(obj) {
    obj.parent = this;
    this.children.add(obj);
  }
  update(t) {
    this.children.forEach((ele) => {
      ele.update(t);
    });
  }
}

add 添加的 obj 是一个时间轨对象(Track)，update 调用的也是时间轨对象，作用就是放置多个时间轨对象(Track)

类:Track

用处

用来绘制补间动画，即两个时间点，有不同的状态，从状态一到状态二的变化过程。

代码

export default class Track {
  constructor(target) {
    this.target = target; // 时间轨对象
    this.parent = null;
    this.start = 0; // 时间轨开始时间
    this.timeLen = 5; // 单次时间轨跑完的时间
    this.loop = false; // 是否循环
    this.keyMap = new Map();
    /** 
     * 存那些时间点状态，大概结构为[
        [
          "a",
          [
            [500, a],
            [1000, 0],
            [1500, a],
          ],
        ],
      ]
      */
    this.onEnd = () => {};
    this.prevTime = 0;
  }
  update(t) {
    const { keyMap, timeLen, target, loop, start, prevTime } = this;
    let time = t - start; // 已经过去的时间
    if (timeLen >= prevTime && timeLen < time) {
      this.onEnd();
    }
    this.prevTime = time;
    if (loop) {
      time = time % timeLen; // 如果要循环，那就取余，比如我只画了0-2s的动画，时间来到3s的时候，因为我设置了timeLen为2，那么3s的时候其实执行的是1s时候的动画
    }
    for (const [key, fms] of keyMap) {
      const last = fms.length - 1;
      if (time < fms[0][0]) {
        // 当前时间小于动画开始时间，那么直接取第一个状态
        target[key] = fms[0][1];
      } else if (time > fms[last][0]) {
        // 当前时间大于动画结束时间，那么直接取最后一个状态
        target[key] = fms[last][1];
      } else {
        // 根据线性关系均匀变化
        target[key] = getValBetweenFms(time, fms, last);
      }
    }
  }
}

// 这个就和上面返回一个线性关系式是一样的
function getValBetweenFms(time, fms, last) {
  for (let i = 0; i < last; i++) {
    const fm1 = fms[i];
    const fm2 = fms[i + 1];
    if (time >= fm1[0] && time <= fm2[0]) {
      const delta = {
        x: fm2[0] - fm1[0],
        y: fm2[1] - fm1[1],
      };
      const k = delta.y / delta.x;
      const b = fm1[1] - fm1[0] * k;
      return k * time + b;
    }
  }
}

然后大家可以对照星星对你眨眼睛的代码来看一下，是不是就是这么个逻辑

//建立轨道对象
const track = new Track(obj);
track.start = new Date();
track.timeLen = 2000;
track.loop = true;
track.keyMap = new Map([
  [
    "a",
    [
      [500, a],
      [1000, 0],
      [1500, a],
    ],
  ],
]);
compose.add(track);
!(function ani() {
  compose.update(new Date());
  render();
  requestAnimationFrame(ani);
})();

类:Sky

用处

本质上还是只是个容器而已，调用的都是子类Poly的方法

代码

export default class Sky {
  constructor(gl) {
    this.gl = gl;
    this.children = [];
  }
  add(obj) {
    obj.gl = this.gl;
    this.children.push(obj);
  }
  updateVertices(params) {
    this.children.forEach((ele) => {
      ele.updateVertices(params);
    });
  }
  draw() {
    this.children.forEach((ele) => {
      ele.init();
      ele.draw();
    });
  }
}

类:Poly

用处

绘制多边形

代码

const defAttr = () => ({
  gl: null, // 上下文对象
  vertices: [], // 具体的点位数据数组,例如[1,2,3,4,5,6]
  geoData: [], // 根据size分配到的每个点应该有的数据，比如我们size是2，vertices为[1,2,3,4,5,6],那么此时的数据为[{x:1,y:2,...param},{x:3,y:4,...param},{x:5,y:6,...param}],还有其他自定义的参数,由外部定义
  size: 2, // 绘制的时候以几个参数作为一个点
  attrName: "a_Position", // attribute变量名
  uniName: "u_IsPOINTS", // 兼容mac
  count: 0, // 数量
  types: ["POINTS"], // 绘制的类型
  circleDot: false, // 兼容mac
  u_IsPOINTS: null, // 兼容mac
});
export default class Poly {
  constructor(attr) {
    Object.assign(this, defAttr(), attr);
    this.init();
  }
  init() {
    const { attrName, size, gl, circleDot } = this;
    if (!gl) {
      return;
    }
    //缓冲对象
    const vertexBuffer = gl.createBuffer();
    //绑定缓冲对象
    gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
    //写入数据
    this.updateBuffer();
    //获取attribute 变量
    const a_Position = gl.getAttribLocation(gl.program, attrName);
    //修改attribute 变量
    gl.vertexAttribPointer(a_Position, size, gl.FLOAT, false, 0, 0);
    //赋能-批处理
    gl.enableVertexAttribArray(a_Position);
    //如果是圆点，就获取一下uniform 变量
    if (circleDot) {
      this.u_IsPOINTS = gl.getUniformLocation(gl.program, "u_IsPOINTS");
    }
  }
  // 更新缓冲区对象
  updateBuffer() {
    const { gl, vertices } = this;
    this.updateCount();
    gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
  }
  // 更新点的数量
  updateCount() {
    this.count = this.vertices.length / this.size;
  }
  // 新增点
  addVertice(...params) {
    this.vertices.push(...params);
    this.updateBuffer();
  }
  // 删除点
  popVertice() {
    const { vertices, size } = this;
    const len = vertices.length;
    vertices.splice(len - size, len);
    this.updateCount();
  }
  // 设置点
  setVertice(ind, ...params) {
    const { vertices, size } = this;
    const i = ind * size;
    params.forEach((param, paramInd) => {
      vertices[i + paramInd] = param;
    });
  }
  // 更新点
  updateVertices(params) {
    const { geoData } = this;
    const vertices = [];
    geoData.forEach((data) => {
      params.forEach((key) => {
        vertices.push(data[key]);
      });
    });
    this.vertices = vertices;
  }
  draw(types = this.types) {
    const { gl, count, circleDot, u_IsPOINTS } = this;
    for (let type of types) {
      circleDot && gl.uniform1f(u_IsPOINTS, type === "POINTS");
      gl.drawArrays(gl[type], 0, count);
    }
  }
}

然后我们拿狮子座的代码来理解一下这个Poly类

//夜空
const sky = new Sky(gl);
//建立合成对象
const compose = new Compose();

//正在绘制的多边形
let poly = null;
//鼠标划上的点
let point = null;

canvas.addEventListener("mousedown", (event) => {
  if (event.button === 2) {
    popVertice();
  } else {
    const { x, y } = getMousePosInWebgl(event, canvas);
    if (poly) {
      addVertice(x, y);
    } else {
      crtPoly(x, y);
    }
  }
  render();
});

canvas.addEventListener("mousemove", (event) => {
  const { x, y } = getMousePosInWebgl(event, canvas);
  point = hoverPoint(x, y);
  canvas.style.cursor = point ? "pointer" : "default";
  if (poly) {
    const obj = poly.geoData[poly.geoData.length - 1];
    obj.x = x;
    obj.y = y;
  }
});

!(function ani() {
  compose.update(new Date());
  sky.updateVertices(["x", "y", "pointSize", "alpha"]);
  render();
  requestAnimationFrame(ani);
})();

function crtPoly(x, y) {
  let o1 = point ? point : { x, y, pointSize: random(), alpha: 1 };
  const o2 = { x, y, pointSize: random(), alpha: 1 };
  poly = new Poly({
    size: 4,
    attrName: "a_Attr",
    geoData: [o1, o2],
    types: ["POINTS", "LINE_STRIP"],
    circleDot: true,
  });
  sky.add(poly);
  crtTrack(o1);
  crtTrack(o2);
}

function addVertice(x, y) {
  const { geoData } = poly;
  if (point) {
    geoData[geoData.length - 1] = point;
  }
  let obj = { x, y, pointSize: random(), alpha: 1 };
  geoData.push(obj);
  crtTrack(obj);
}

function popVertice() {
  poly.geoData.pop();
  const { children } = compose;
  const last = children[children.length - 1];
  children.delete(last);
  poly = null;
}

上面的代码只用到了·geoData·，而前面我们绘制内容的时候也用到了·vertices·

类:ShapeGeo

用处

根据轨迹点图形得到能涂满颜色的多个三角形，核心逻辑还是那几个
1.寻找满足以下条件的▲ABC：
▲ABC的顶点索引位置连续，如012,123、234
点C在向量AB的正开半平面里，可以理解为你站在A点，面朝B点，点C要在你的左手边
▲ABC中没有包含路径G 中的其它顶点
2.当找到▲ABC 后，就将点B从路径的顶点集合中删掉，然后继续往后找。
3.当路径的定点集合只剩下3个点时，就结束。
4.由所有满足条件的▲ABC构成的集合就是我们要求的独立三角形集合。

这下面的方式就是按照上面的核心逻辑来的

代码

export default class ShapeGeo {
  constructor(pathData=[]) {
    this.pathData = pathData;
    this.geoData = [];
    this.triangles = [];
    this.vertices = [];
    this.parsePath();
    this.update();
  }
  update() {
    this.vertices = [];
    this.triangles = [];
    this.findTriangle(0);
    this.upadateVertices()
  }
  parsePath() {
    this.geoData = [];
    const { pathData, geoData } = this
    for (let i = 0; i < pathData.length; i += 2) {
      geoData.push({ x: pathData[i], y: pathData[i + 1] })
    }
  }
  findTriangle(i) {
    const { geoData, triangles } = this;
    const len = geoData.length;
    // 当路径的定点集合只剩下3个点时，就结束。
    if (geoData.length <= 3) {
      triangles.push([...geoData]);
    } else {
      // ▲ABC的顶点索引位置连续
      const [i0, i1, i2] = [
        i % len,
        (i + 1) % len,
        (i + 2) % len
      ];
      const triangle = [
        geoData[i0],
        geoData[i1],
        geoData[i2],
      ];
      /** 
       * 点C在向量AB的正开半平面里，可以理解为你站在A点，面朝B点，点C要在你的左手边,也就是这里的函数
        this.cross要大于0，
        ▲ABC中没有包含路径G 中的其它顶点，也就是这里的!this.includePoint(triangle)
       * 
       * 
       * */ 
      if (this.cross(triangle) > 0 && !this.includePoint(triangle)) {
        // 当找到▲ABC 后，就将点B(第二个点，也就是i1)从路径的顶点集合中删掉，然后继续往后找。
        triangles.push(triangle);
        geoData.splice(i1, 1);
      }
      // 如果我们找到了那个三角形的话，这里的i1，就不是原来的那个点开始了哦，而是从后面那个点开始了。
      this.findTriangle(i1);
    }
  }
  includePoint(triangle) {
    for (let ele of this.geoData) {
      if (!triangle.includes(ele)) {
        if (this.inTriangle(ele, triangle)) {
          return true;
        }
      }
    }
    return false;
  }
  inTriangle(p0, triangle) {
    let inPoly = true;
    for (let i = 0; i < 3; i++) {
      const j = (i + 1) % 3;
      const [p1, p2] = [triangle[i], triangle[j]];
      if (this.cross([p0, p1, p2]) < 0) {
        inPoly = false;
        break
      }
    }
    return inPoly;
  }
  cross([p0, p1, p2]) {
    const [ax, ay, bx, by] = [
      p1.x - p0.x,
      p1.y - p0.y,
      p2.x - p0.x,
      p2.y - p0.y,
    ];
    return ax * by - bx * ay;
  }
  upadateVertices() {
    const arr = []
    // 由所有满足条件的▲ABC构成的集合就是我们要求的独立三角形集合。
    this.triangles.forEach(triangle => {
      for (let { x, y } of triangle) {
        arr.push(x, y)
      }
    })
    this.vertices = arr
  }
}

大概的逻辑我在上面都写了注释，接下来再讲讲一些晦涩难懂的函数，比如，正半区为什么可以使用cross(...param)>0
这里其实使用了向量的差积的理解
矢量叉积的知识：

设矢量P = ( x1, y1 )，Q = ( x2, y2 )，则矢量叉积定义为由(0,0)、p1、p2和p1+p2所组成的平行四边形的带符号

的面积，即：P × Q = x1y2 - x2y1，其结果是一个标量。显然有性质 P × Q = - ( Q × P ) 和 P × ( - Q )

= - ( P × Q )。一般在不加说明的情况下，本文下述算法中所有的点都看作矢量，两点的加减法就是矢量相加减，而点的乘法则看作矢量叉积。

叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：
若 P × Q > 0 , 则Q在P的逆时针方向。
若 P × Q < 0 , 则Q在P的顺时针方向。
若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。

结语

本篇文章就到这里结束了，更多内容敬请期待，债见~

blog-of-codesigner(顾炯洋)

recorded growth

前言