微信小程序版本更新提示

前言

本篇将详细的带大家了解一下视图矩阵。

视图矩阵本质

我们之前说过，视图矩阵可以让我们从另一个角度观察物体。

那我们能不能在没有视图矩阵的情况下，看见物体的另一个角度呢？

答案肯定是可以，我们自己用模型矩阵把物体转一下就可以了。

因此，视图矩阵的本质是对物体的旋转变换。

而物体变换的本质则是对物体顶点的位移。

所以，接下来咱们就通过模型矩阵的旋转变换来理解视图矩阵。

1.我在webgl 画一个立方体

2.默认我们只能看见这个立方体的正面。

3.我想看看立方体右侧长啥样。

我们要实现第3步，可以构建一个矩阵，让它对立方体的顶点进行变换。

这个矩阵的构建思路有两条：

构建一个从左前方看物体的视图矩阵
构建一个让立方体向左旋转的模型矩阵
上面的两个矩阵最终的因子形态都是一样的。

接下来我就按照上面的两个思路建立两个矩阵，然后对这两个矩阵的因子做一下对比，若它们都是一样的，那大家也就可以理解视图矩阵的本质了。

构建视图矩阵

首先咱们先准备一个场景。

我们通过俯视图来解释这个场景。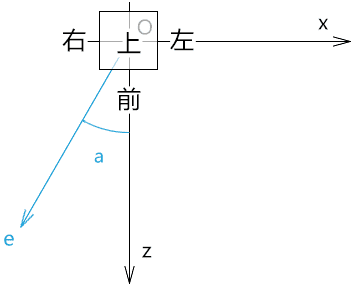

已知：

• 视点为e
• 目标点t=原点O
• 上方向u(0,1,0)
  求：视点e所见的物体的形态

接下来我们先以模型矩阵求解。

构建模型矩阵

基于视线和z轴的夹角，将立方体向左旋转a即可。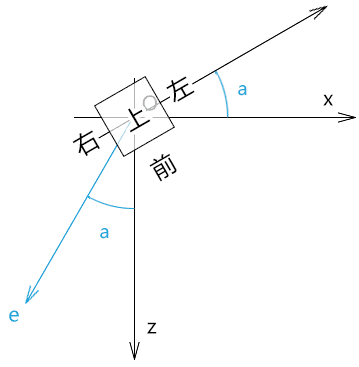

想象一下，现在我们站在z轴上看见的立方体的形态，就相当于我们之前视点在e上算看见的立方体的形态。
1.建立视线，目标点和上方向

e=(-0.5, 0, 1)
t=(0, 0, 0)
u=(0, 1, 0)

2.用目标点减视点得视线c

c=e-t
c=(-0.5, 0, 1)

3.将c 归一化后，可得角a 的正弦值和余弦值

|c|=sqrt(c.x*c.x+c.y*c.y+c.z*c.z)

c.x=c.x*(1/|c|)
c.y=0
c.z=c.z*(1/|c|)
         
cos = c.z
sin = c.x

4.上面的cos和sin 便可以作为立方体向左旋转的模型矩阵(列主序)的旋转因子

const modelMatrix = [
    cos,  0, sin, 0,
    0,    1, 0,   0,
    -sin, 0, cos, 0,
    0,    0, 0,   1
]

接下来将模型矩阵传给顶点着色器，让其与顶点相乘即可，其原理我们在说模型矩阵的时候都说过，我就不再多说了。

效果如下：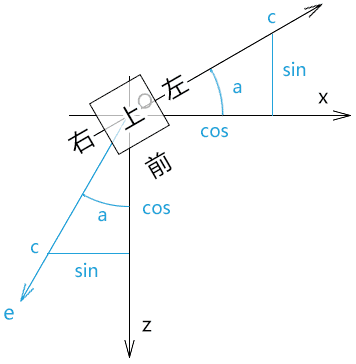

const e = new Vector3(-0.5, 0, 1)
const t = new Vector3(0, 0, 0)
const u = new Vector3(0, 1, 0)

const c = new Vector3().subVectors(e, t)
c.normalize()

const cos = c.z
const sin = c.x

const modelMatrix = [
    cos, 0, sin, 0,
    0, 1, 0, 0,
    -sin, 0, cos, 0,
    0, 0, 0, 1
]

构建视图矩阵

我们要构建视图矩阵，就得构建新的坐标系[O;a,b,c]。

1.新坐标系的z 轴，视线c 的归一化。

c=(sin,0,cos)

2.新坐标系的x轴，可视之为上方向u(0,1,0)和视线c(sin,1,cos)构成的平面的垂线的归一化a
a的坐标值可由垂直向量的叉乘定理得出：

a=u^c
a=(0,1,0)^(sin,1,cos)

a.x=u.y*c.z-u.z*c.y
a.x=1*cos-0*1
a.x=cos

a.y=u.z*c.x-u.x*c.z
a.y=0*sin-0*cos
a.y=0

a.z=u.x*c.y-u.y*c.x
a.z=0*1-1*sin
a.z=-sin

因为：向量a是由两个相互垂直的归一化向量的叉乘得出

所以：

|a|=|u|*|c|*sin90°
|a|=1*1*1
|a|=1

所以：向量a 无需再做归一化处理
3.新坐标系的y轴，可视之为视线c(sin,0,cos)和向量a(cos,0,-sin)构成的平面的垂线的归一化b

b=c^a
b=(sin,0,cos)^(cos,0,-sin)

b.x=c.y*a.z-c.z*a.y
b.x=0*-sin-cos*0
b.x=0

b.y=c.z*a.x-c.x*a.z
b.y=cos*cos+sin*sin
b.y=1

b.z=c.x*a.y-c.y*a.x
b.z=sin*0-0*cos
b.z=0

向量b无需归一，原理同上
4.综上所述，新坐标系的三个基向量分别为：

a(cos,0,-sin)
b(0,1,0)
c(sin,0,cos)

5.根据三个基向量构建视图矩阵(列主序)

const viewMatrix = [
    cos,  0, sin, 0,
    0,    1, 0,   0,
    -sin, 0, cos, 0,
    0,    0, 0,   1
]

将视图矩阵viewMatrix和模型矩阵modelMatrix对比一下，会发现，它们是一样的。

所以：视图矩阵的本质是对物体的旋转变换。

代码实现：

const e = new Vector3(-0.5, 0, 1)
const t = new Vector3(0, 0, 0)
const u = new Vector3(0, 1, 0)

const c = new Vector3().subVectors(e, t)
c.normalize()
const a = new Vector3().crossVectors(u, c)
a.normalize()
const b = new Vector3().crossVectors(c, a)
b.normalize()

const viewMatrix = [
    a.x, b.x, c.x, 0,
    a.y, b.y, c.y, 0,
    a.z, b.z, c.z, 0,
    0, 0, 0, 1
]

结语

本篇文章就到这里了，更多内容敬请期待，债见~