【可视化学习】72-从入门到放弃WebGL(九)
发表于：2024-06-28 |

前言

本篇将继续学习WebGL的内容

GLSL语法测试

在GLSL ES中，我们是没法像js中一样，调试的时候，只需要console.log就可以把我们的数据给打印出来。

GLSL ES数据的输出

我现在片元着色器里写了一个4维向量的加法运算，我想把它打印出来看看v 的结果是不是如我想的那样。

1
2
3
4
5
6
7
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    vec4 v=vec4(1,2,3,4)+vec4(5,6,7,8);
    void main(){
      ……
    }
</script>

我们知道，这个向量相加的结果应该是一个新的向量(1+5,2+6,3+7,4+8)，答案为(6,8,10,12)

这里我们可以通过先把GLSL ES 数据画到画布中，然后再从画布的像素数据中解析出GLSL ES 数据的方式实现一个类似console.log的效果

1
2
3
4
5
6
7
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    vec4 v=vec4(1,2,3,4)+vec4(5,6,7,8);
    void main(){
      gl_FragColor=v/255.0;
    }
</script>

因为gl_FragColor 中1个单位的分量就相当于canvas画布中255的分量值，所以我让上面的向量v直接除以255。

注：此方法只适用于向量因子在0-255的数据。我们在此先不考虑太深，先把语法跑通。

我们可以先在画布中画一个点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    void main(){
      gl_Position=a_Position;
      gl_PointSize=512.0;
    }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    vec4 v=vec4(1,2,3,4)+vec4(5,6,7,8);
    void main(){
      gl_FragColor=v/255.0;
    }
</script>

效果如下：
效果图
接下来我们就可以获取canvas 画布中的像素数据了。

在canvas 画布中获取像素数据

在此先给会canvas 2d 的同学提一下，在我们通过canvas.getContext() 方法获取2d或webgl 上下文对象的同时，也决定了canvas画布的命运。

canvas.getContext(‘2d’) 方法会让canvas画布变成2d画布，2d的canvas画布可以通过ctx.getImageData() 方法获取画布中的像素；

canvas.getContext(‘webgl’) 方法会让canvas画布变成webgl画布，webgl画布需要通过ctx.readPixels() 方法获取画布中的像素。

1.建立一个8位无符号型数组，用于存储一个像素的数据。

1
const pixel = new Uint8Array(4);

2.从画布中采集一个像素出来。

1
2
3
4
5
6
7
8
9
gl.readPixels(
    canvas.width / 2,
    canvas.height / 2,
    1,
    1,
    gl.RGBA,
    gl.UNSIGNED_BYTE,
    pixel
);

gl.readPixels(x, y, width, height, format, type, pixels)

  • x, y：从哪里采集像素
  • width, height：采集多大一块区域的像素
  • format：数据格式
  • type：数据类型
    • gl.UNSIGNED_BYTE
    • gl.UNSIGNED_SHORT_5_6_5
    • gl.UNSIGNED_SHORT_4_4_4_4
    • gl.UNSIGNED_SHORT_5_5_5_1
    • gl.FLOAT
  • pixels：装像素的容器
    • Uint8Array 对应 gl.UNSIGNED_BYTE
    • Uint16Array 对应 gl.UNSIGNED_SHORT_5_6_5, gl.UNSIGNED_SHORT_4_4_4_4, 或者 gl.UNSIGNED_SHORT_5_5_5_1
    • Float32Array 对应 gl.FLOAT

3.打印pixel

1
console.log(pixel); //Uint8Array(4) [6, 8, 10, 12]

效果图

打印多个向量

1.用不同的向量数据画圆环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
<!-- 顶点着色器 -->
<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    void main(){
        gl_Position=a_Position;
        gl_PointSize=512.0;
    }
</script>
<!-- 片元着色器 -->
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    mat4 m=mat4(
      255,0,0,255,
      255,255,0,255,
      0,255,0,255,
      0,0,255,255
    );
    void main(){
      float dist=distance(gl_PointCoord,vec2(0.5,0.5));
      if(dist>=0.0&&dist<0.125){
        gl_FragColor=m[0]/255.0;
      }else if(dist>=0.125&&dist<0.25){
        gl_FragColor=m[1]/255.0;
      }else if(dist>=0.25&&dist<0.375){
        gl_FragColor=m[2]/255.0;
      }else if(dist>=0.325&&dist<0.5){
        gl_FragColor=m[3]/255.0;
      }else{
        discard;
      }
    }
</script>

如图所示
效果图

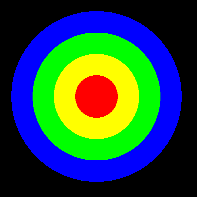
2.按照比例关系从四个圆环中取色

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const vw = 512 / 8;
for (let i = 0; i < 4; i++) {
    logPixel(vw * i + vw / 2)
}

function logPixel(offset = 0) {
    //建立像素集合
    let pixel = new Uint8Array(4);
    //从缓冲区读取像素数据，然后将其装到事先建立好的像素集合里
    gl.readPixels(
        canvas.width / 2 + offset,
        canvas.height / 2,
        1,
        1,
        gl.RGBA,
        gl.UNSIGNED_BYTE,
        pixel
    );
    console.log(pixel);
}

效果图
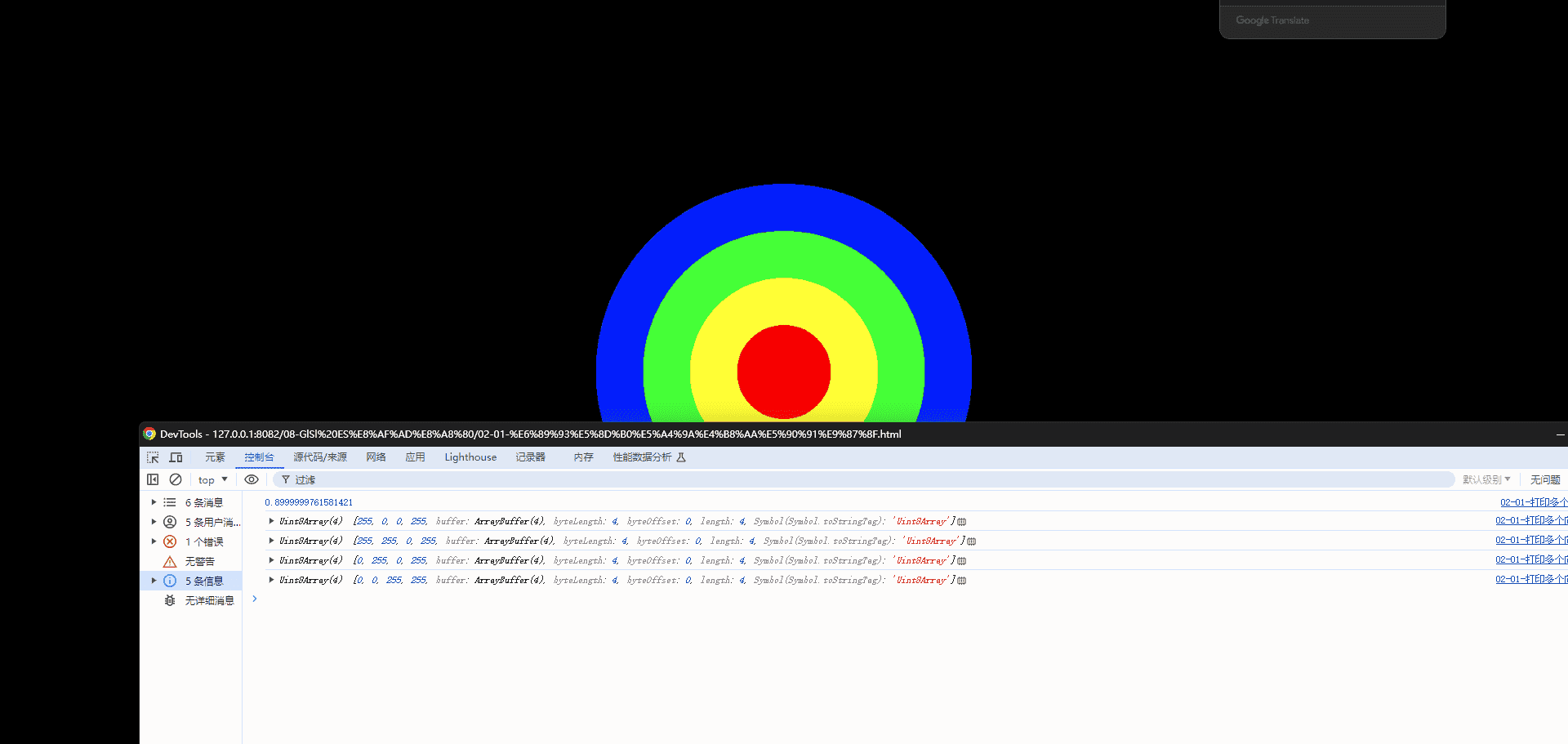
上面这种方式，在特定的一些高分辨率设备上，会出现兼容性问题，画出来的圆会比较小，取样会失败

打印多个向量-适配不同分辨率的设备

我接下来会基于片元位置和画布的宽高比绘图，然后再基于这样的比例取样。
1.绘制一个充满画布的矩形面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const source = new Float32Array([
    -1, 1,
    -1, -1,
    1, 1,
    1, -1
]);

const rect = new Poly({
    gl,
    source,
    type: 'TRIANGLE_STRIP',
    attributes: {
        a_Position: {
            size: 2,
            index: 0
        }
    },
    uniforms: {
        u_CanvasSize: {
            type: 'uniform2fv',
            value: [canvas.width, canvas.height]
        }
    }
})

gl.clear(gl.COLOR_BUFFER_BIT);
rect.draw()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
<!-- 顶点着色器 -->
<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    void main(){
      gl_Position=a_Position;
    }
</script>
<!-- 片元着色器 -->
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    uniform vec2 u_CanvasSize;
    float halfW=u_CanvasSize.x/2.0;
    float halfH=u_CanvasSize.y/2.0;
    void main(){
      mat4 m=mat4(
        255,0,0,255,
        255,255,0,255,
        0,255,0,255,
        0,0,255,255
      );
      bool xb= gl_FragCoord.x<halfW;
      bool yb= gl_FragCoord.y<halfH;
      if(yb){
        if(xb){
          gl_FragColor=m[0]/255.0;
        }else{
          gl_FragColor=m[1]/255.0;
        }
      }else{
        if(xb){
          gl_FragColor=m[2]/255.0;
        }else{
          gl_FragColor=m[3]/255.0;
        }
      }
    }
</script>

效果
2.用js取上面四个格子的中点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const [w, h] = [2, 2]
for (let y = 0; y < 2; y++) {
    for (let x = 0; x < 2; x++) {
        const px = canvas.width * (x + 0.5) / w
        const py = canvas.height * (y + 0.5) / h
        logPixel(px, py)
    }
}
function logPixel(x, y) {
    const pixel = new Uint8Array(4)
    gl.readPixels(
        x, y,
        1, 1,
        gl.RGBA,
        gl.UNSIGNED_BYTE,
        pixel
    )
    console.log(pixel)
}

效果

GLSL ES 概述和基本规范

GLSL ES是在GLSL（OpenGL着色器语言）的基础上，删除和简化了一部分功能后形成的，ES版本主要降低了硬件功耗，减少了性能开销。

实际上WebGL并不支持GLSL ES的所有特性，所以大家以后在WebGL API里可能会遇到部分参数无效的情况。

GLSL ES 是写在着色器中的，其具备以下基本规范：

  1. 大小写敏感
  2. 语句末尾必须要有分号
  3. 以main函数为主函数
  4. 注释语法和js 一样
    单行: //
    多行: /**/
  5. 基本数据类型：
    数字型
    浮点型 float，如1.0
    整型 int，如1
    布尔型 bool
    true
    false

变量

声明变量的方法

GLSL ES是强类型语言，在声明变量的时候应该指明变量类型，如：

1
2
3
float f=1.0;
int i=1;
bool b=true;

变量命名规范

  • 只能包括a-z,A-Z,0-9,_
  • 变量名首字母不能是数字
  • 不能是GLSL 关键字，如attribute,vec4,bool
  • 不能是GLSL 保留字，如cast,class,long
  • 不能以下单词开头：gl_, webgl_, webgl

变量的赋值

变量使用等号=赋值，=两侧的数据类型需要一致。

1
2
3
4
int i=8; // ✔
int i=8.0; // ✖
float f=8; // ✖
float f=8.0; // ✔

变量的类型转换

有时候，我们需要将类型a 的数据转成类型b 的数据，交给类型为b 的变量。

比如，我要把整形数字转成浮点型交给浮点型变量：

1
float f=float(8)

上面的float() 方法便是类型转换方法。

基础数据的转换有以下几种：

  • 浮点转整数：int(float)
  • 布尔转整数：int(bool)
  • 整数转浮点：float(int)
  • 布尔转浮点：float(bool)
  • 整数转布尔：bool(int)
  • 浮点转布尔：bool(float)

向量

向量类型

GLSL ES 支持2、3、4维向量，根据分量的数据类型，向量可以分为3类：

vec2、vec3、vec4：分量是浮点数
ivec2、ivec3、ivec4：分量是整数
bvec2、bvec3、bvec4：分量是布尔值

向量的创建

在GLSL ES 中，向量占有很重要的地位，所以GLSL ES为其提供了非常灵活的创建方式。
比如:

1
2
3
vec3 v3 = vec3(1.0, 0.0, 0.5);   // (1.0, 0.0, 0.5)
vec2 v2 = vec2(v3);              // (1.0, 0.0) 
vec4 v4 = vec4(1.0);             // (1.0,1.0,1.0,1.0)

我们还可以将多个向量合在一起：

1
vec4 v4b=vec4(v2,v4);             // (1.0,0.0,1.0,1.0)

注：= 两侧的数据类型必须一致，比如下面的写法会报错：

1
vec4 v4 = vec2(1.0);   //错的

向量分量的访问

向量分量的访问方式：
1.通过分量属性访问

1
2
3
v4.x, v4.y, v4.z, v4.w  // 齐次坐标
v4.r, v4.g, v4.b, v4.a  // 色值
v4.s, v4.t, v4.p, v4.q  // 纹理坐标

2.将分量的多个属性连在一起，可以获取多个向量

1
2
3
4
vec4 v4 = vec4(1.0,2.0,3.0,4.0); 
v4.xy //(1.0,2.0)
v4.yx //(2.0,1.0)
v4.xw //(1.0,4.0)

3.通过分量索引访问

1
v4[0], v4[1], v4[2], v4[3]

用上面的方法访问到向量后，也可以用=号为向量赋值。

1
2
3
v4.x=1.0
v4[0]=1.0
v4.xy=vec2(1.0,2.0)

矩阵

矩阵的类型

GLSL ES 支持2、3、4维矩阵：

  • mat2
  • mat3
  • mat4
    矩阵中的元素都是浮点型。

矩阵的建立

GLSL ES 中的矩阵是列主序的，在建立矩阵的时候，其参数结构有很多种。
1.浮点数，其参数是按照列主序排列的。

1
2
3
4
5
6
7
8
9
10
11
12
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
/*
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
*/

2.向量

1
2
3
4
5
6
7
8
9
10
11
12
13
vec4 v4_1=vec4(1,2,3,4);
vec4 v4_2=vec4(5,6,7,8);
vec4 v4_3=vec4(9,10,11,12);
vec4 v4_4=vec4(13,14,15,16);
mat4 m=mat4(v4_1,v4_2,v4_3,v4_4);
/*
[
    1,2,3,4,
    5,6,7,8,
    9,10,11,12,
    13,14,15,16
]    
*/

3.浮点+向量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vec4 v4_1=vec4(1,5,9,13);
vec4 v4_2=vec4(2,6,10,14);
mat4 m=mat4(
    v4_1,
    v4_2,
    3,7,11,15,
    4,8,12,16
);
/*
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16   
*/

4.单个浮点数

1
2
3
4
5
6
7
8
9
mat4 m=mat4(1);
/*
[
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0,
    0, 0, 0, 1,
]    
*/

注：如矩阵中的参数数量大于1，小于矩阵元素数量，会报错

1
2
mat4 m4 = mat4(1.0,2.0);
/*报错*/

矩阵的访问

1.使用[] 可以访问矩阵的某一行。

1
2
3
4
5
6
7
8
9
10
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
m[0]
/*
    1,5,9,13,
*/

2.使用 m[y][x] 方法，可以访问矩阵第y行，第x列的元素。

1
2
3
4
5
6
7
8
9
10
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
m[0][0]
/* 1 */
m[2][1]
/* 3 */

3.m[y] 可以理解为一个向量，其内部的元素，可以像访问向量元素一样去访问。

1
2
3
4
5
6
7
8
9
10
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
m[0].[0] //1
m[0].x //1
m[0].r //1
m[0].s //1

注：我们在此要注意一下[] 中索引值的限制。

[] 中的索引值只能通过以下方式定义：

1.整形字面量，如0，1，2，3

1
2
m[0]
m[1]

2.用const 修饰的变量

1
2
const int y=0;
m[y];

注：以下写法是错误的

1
2
int y=0;
m[y];

3.循环索引

1
2
3
4
5
6
7
8
9
10
11
12
13
mat4 n=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
mat4 m=mat4(1);
void main(){
    for(int i=0;i<4;i++){
        m[i]=n[i];
    }
    ……
}

前面三项组成的表达式

1
2
const int y=0;
m[y+1];

运算符

算数运算符

运算符 描述 例子
+ 加法 x = y + 2
- 减法 x = y - 2
* 乘法 x = y * 2
/ 除法 x = y / 2
++ 自增 x = ++y
x = y++
– 自减 x = –y
x = y–

赋值运算符

运算符 描述 例子
= 赋值等于 x = y
+= 加等于 x += y
-= 减等于 x -= y
*= 乘等于 x *= y
/= 除等于 x /= y

比较运算符

运算符 描述 例子
== 等于 x == 8
!= 不等于 x != 8
> 大于 x > 8
< 小于 x < 8
>= 大于或等于 x >= 8
<= 小于或等于 x <= 8

条件运算符

语法 例子
布尔 ?值1:值2 float f=2>3?1.0:2.0;

逻辑运算符

这里md的table里面我打不出或的||,就用了俩个1替代

运算符 描述 例子
&& 和 true&&true=true;
11 或 false11true=true; true11true=true;
! 非 !false=true;
^^ 异或

向量运算

向量可以与以下数据进行各种运算：

  • 单独数字
  • 向量
  • 矩阵

向量和单独数字的运算

向量可以与单独数字进行加减乘除。

1
2
3
4
5
vec4 v=vec4(1,2,3,4);
v+=1.0;
v-=1.0;
v*=2.0;
v/=2.0;

上面的计算结果分别为，我这里都是以向量(1，2，3，4)为基底，不是一步步算下来的

向量与数字相加

相当于每位都加上这个数字

1
(1+1,2+1,3+1,4+1)=(2,3,4,5)

向量与数字相减

相当于每位都减去这个数字

1
(1-1,2-1,3-1,4-1)=(0,1,2,3)

向量与数字相乘

相当于每位都乘以这个数字

1
(1*2,2*2,3*2,4*2)=(2,4,6,8)

向量与数字相除

相当于每位都除以这个数字

1
(1/2,2/2,3/2,4/2)=(0.5,1,1.5,2)

概念

vec4 是浮点型向量。

我们上例中，写在vec4() 中的整数可以被vec4() 方法转换成浮点数。

vec4 向量在做四则运算时，其用于运算的数字类型应该是浮点型。

比如，下面的写法会报错：

1
v+=1;

整型向量ivec2、ivec3、ivec4 的运算原理同上。

向量和向量的运算

1
2
3
4
5
6
vec4 p=vec4(1,2,3,4);
vec4 v=vec4(2,4,6,8);
v+=p;
v-=p;
v*=p;
v/=p;

这次接下来我按照顺序计算

向量相加

两个向量相加就是按位数依次相加

1
(1+2,2+4,3+6,4+8)=(3,6,9,12)

向量相减

两个向量相减就是按位数依次相减

1
(3-1,6-2,9-3,12-4)=(2,4,6,8)

向量相乘

两个向量相乘就是按位数依次相乘

1
(2*1,4*2,6*3,8*4)=(2,8,18,32)

向量相除

两个向量相除就是按位数依次相除

1
(2/1,8/2,18/3,32/4)=(2,4,6,8)

向量距离

这里也展开说一下向量距离的计算公式

逻辑

每一位依次按位相减的平方，相加之后开平方

1
Math.sqrt((2-1)^2+(4-2)^2+(6-3)^2+(8-4)^2)
GLSL ES简写
1
distance(p0,p1) 向量距离

向量点积

逻辑

每一位相乘并相加，实际上他的值是一个常数，结果就是21+42+63+84=2+8+18+32

GLSL ES简写
1
dot(p0,p1) 点积

向量叉积

逻辑

。向量叉乘公式原理是向量c的方向与a,b所在的平面垂直，且方向要用“右手法则”判断。具体公式为：|向量c|=|向量a×向量b|=|a||b|sin<a,b>，其中<a,b>表示向量a和b之间的夹角。
右手法则

GLSL ES简写
1
cross(p0,p1) 叉乘

向量与矩阵的运算

矩阵只能与向量进行乘法运算。

向量乘以矩阵和矩阵乘以向量的结果是不一样的，但数据类型都是向量。

矩阵乘以向量

1
2
3
4
5
6
7
8
9
10
11
12
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
vec4 p=vec4(1,2,3,4);
vec4 v=m*p;

/*
    [30, 70, 110, 150]
*/

以v.x为例说一下其算法：

1
2
3
4
v.x=m[0][0]*v.x+m[1][0]*v.y+m[2][0]*v.z+m[3][0]*v.w
v.x=1*1+2*2+3*3+4*4
v.x=1+4+9+16
v.x=30

可能这个不太好理解，那是因为代码里面是列主序的矩阵，我们把它变成行主序的矩阵，就和我们在大学学的就一样了。

此时的我们四维矩阵就是

1
2
3
4
1  2  3  4
5  6  7  8
9  10 11 12
13 14 15 16

对应的向量则是

1
2
3
4
1 
2 
3 
4

我们让矩阵的每一行的值按照顺序相乘并相加，可以得到

1
2
3
4
1*1+2*2+3*3+4*4=30
5*1+2*6+3*7+4*8=70
9*1+2*10+3*11+4*12=110
13*1+14*2*15*3+16*4=150

得到的结果就是

1
2
3
4
30
70
110
150

又因为这是我们之前根据行主序算的，所以变成列主序要变成它的转置矩阵，也就是将矩阵的行列互换得到的新矩阵称为转置矩阵，转置矩阵的行列式不变

1
[30 70 110 150]

这个就是最终的结果了

矩阵运算

矩阵可以与以下数据进行各种运算：

  • 单独数字
  • 向量
  • 矩阵

矩阵和单独数字的运算

1
2
3
4
5
6
7
8
9
10
mat4 m=mat4(
    1,5,9,13,
    2,6,10,14,
    3,7,11,15,
    4,8,12,16
);
m+=1.0;
m-=1.0;
m*=2.0;
m/=2.0;

这里和之前的向量部分是一样的，就是每一位都进行加减乘除就可以了,我就不展开了

矩阵和向量的运算

这里在上面向量和矩阵计算说过了，就不多阐述了

矩阵和矩阵的运算

1
2
3
4
5
6
7
8
9
10
11
12
mat4 m=mat4(
    2,16,8,8,
    4,8,8,8,
    8,4,8,8,
    16,8,8,8
);
mat4 n=mat4(
    1,4,1,2,
    2,4,2,1,
    4,4,1,2,
    8,4,2,1
);

比如我们有上面这样的俩个矩阵（列主序）

矩阵相加

这个很简单，就是把参数按照索引一个个都给加起来

1
2
3
4
5
6
7
8
m+=n;

/*
    3, 20, 9, 10,
    6, 12, 10, 9,
    12, 8, 9, 10,
    24, 12, 10, 9,
*/

矩阵减法

相同索引位置的元素相减

1
2
3
4
5
6
7
m-=n;
/*
    1, 12, 7, 6,
    2, 4, 6, 7,
    4, 0, 7, 6,
    8, 4, 6, 7,
*/

矩阵除法

相同索引位置的元素相除

1
2
3
4
5
6
7
m/=n;
/*
    2, 4, 8, 4,
    2, 2, 4, 8,
    2, 1, 8, 4,
    2, 2, 4, 8,
*/

矩阵乘法

1
2
3
4
5
6
7
m*=n;
/*
    58, 68, 64, 64,
    52, 80, 72, 72,
    64, 116, 88, 88,
    64, 176, 120, 120,
*/

这个和上面的向量乘以矩阵是一样的，就是对应行乘以对应列然后相加,这里拿第一列作为参考，列主序的矩阵是每一列乘以每一行，行主序的矩阵是每一行乘以每一列，记住这个就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
m[0][0]=m[0][0]*n[0][0]+m[1][0]*n[0][1]+m[2][0]*n[0][2]+m[3][0]*n[0][3]
m[0][0]=2*1+4*4+8*1+16*2
m[0][0]=58

m[1][0]=m[0][0]*n[1][0]+m[1][0]*n[1][1]+m[2][0]*n[1][2]+m[3][0]*n[1][3]
m[1][0]=2*2+4*4+8*2+16*1
m[1][0]=52

m[2][0]=m[0][0]*n[2][0]+m[1][0]*n[2][1]+m[2][0]*n[2][2]+m[3][0]*n[2][3]
m[2][0]=2*4+4*4+8*1+16*2
m[2][0]=64

m[3][0]=m[0][0]*n[3][0]+m[1][0]*n[3][1]+m[2][0]*n[3][2]+m[3][0]*n[3][3]
m[3][0]=2*8+4*4+8*2+16*1
m[3][0]=64

struct

struct 翻译过来叫结构体，它类似于js 里的构造函数，只是语法规则不一样。

struct 的建立

1
2
3
4
struct Light{
    vec4 color;
    vec3 pos;
};

上面的struct 类似于js 的function，color和pos 既是结构体的属性，也是其形参。

struct 的实例化

1
2
3
4
Light l1=Light(
    vec4(255,255,0,255),
    vec3(1,2,3)
);

上面的vec4()和vec3()数据是结构体的实参，分别对应color属性和pos属性。

访问struct 实例对象中的属性

1
gl_FragColor=l1.color/255.0;

数组

glsl 中的数组具有以下特性：

  • 属于类型数组
  • 只支持一维数组
  • 不支持pop()、push() 等操作
在建立某个类型的数组时，在数据类型后面加[]即可，[]中要写数组的长度：
1
2
3
vec4 vs[2];
vs[0]=vec4(1,2,3,4);
vs[1]=vec4(5,6,7,8);
数组的长度需要按照以下方式定义：

1.整形字面量

1
vec4 vs[2];

2.const 限定字修饰的整形变量

1
2
const int size=2;
vec4 vs[size];

3.不能是函数的参数

数组需要显示的通过索引位置一个元素、一个元素的赋值。
1
2
vs[0]=vec4(1,2,3,4);
vs[1]=vec4(5,6,7,8);
数组中的元素需要用整形的索引值访问
1
gl_FragColor=vs[1]/255.0;

程序流程控制

if判断

glsl 中的if 判断和js 里的if 写法是一样的。都有一套if、else if、else 判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
float dist=distance(gl_PointCoord,vec2(0.5,0.5));

if(dist>=0.0&&dist<0.125){
    gl_FragColor=m[0]/255.0;
}else if(dist>=0.125&&dist<0.25){
    gl_FragColor=m[1]/255.0;
}else if(dist>=0.25&&dist<0.375){
    gl_FragColor=m[2]/255.0;
}else if(dist>=0.375&&dist<0.5){
    gl_FragColor=m[3]/255.0;
}else{
    discard;
}

if 语句写太多会降低着色器执行速度，然而glsl 还没有switch 语句，大家需要注意一下。

for循环

glsl 中的for循环和js类似；

for(初始化表达式; 条件表达式; 循环表达式){

​ 循环体;

}

for循环的基本规则如下：

循环变量只能有一个，只能是int或float 类型。

在循环体中也可以使用break或continue，其功能和js一样。

1
2
3
4
5
6
7
8
9
10
11
float dist=distance(gl_PointCoord,vec2(0.5,0.5));
for(int i=0;i<4;i++){
    float r1=0.125*float(i);
    float r2=r1+0.125;
    if(dist>=r1&&dist<r2){
        gl_FragColor=m[i]/255.0;
        break;
    }else if(i==3){
        discard;
    }
}

上面的循环变量是整形，我们也可以将其变成浮点型：

1
2
3
4
5
6
7
8
9
10
for(float f=0.0;f<=4.0;f++){
    float r1=0.125*f;
    float r2=r1+0.125;
    if(dist>=r1&&dist<r2){
        gl_FragColor=m[int(f)]/255.0;
        break;
    }else if(f==3.0){
        discard;
    }
}

函数

函数的建立

函数类型 函数名(形参){

​ 函数内容;

​ return 返回值;

}

示例

以颜色置灰的方法为例，演示一下函数的用法。

1
2
3
4
5
6
7
8
9
10
11
12
<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    float getLum(vec3 color){
      return dot(color,vec3(0.2126,0.7162,0.0722));
    }
    void main(){
      vec3 color=vec3(255,255,0);
      float lum=getLum(color);
      vec4 v=vec4(vec3(lum),255);
      gl_FragColor=v/255.0;
    }
</script>

上面getLum() 便是获取颜色亮度值的方法。

让一个以rgb为分量的向量color与一套置灰的系数vec3(0.2126,0.7162,0.0722) 进行点积运算，便可得到一个亮度值。

1
dot(color,vec3(0.2126,0.7162,0.0722));

以此亮度值为rgb分量值的颜色便是对初始color 的置灰。

1
2
3
vec3 color=vec3(255,255,0);
float lum=getLum(color);
vec4 v=vec4(vec3(lum),255);

函数的声明

我们也可以将函数体放到其调用方法的后面，不过在调用之前得提前声明函数。

其声明方式如下：

1
2
3
4
5
6
函数类型 函数名(形参类型);
函数名(实参);
函数类型 函数名(形参){
    函数内容;
    return 返回值;
}

我们可以基于之前获取亮度的方法写一下：

1
2
3
4
5
6
7
8
9
10
11
precision mediump float;
float getLum(vec3);
void main(){
    vec3 color=vec3(255,255,0);
    float lum=getLum(color);
    vec4 v=vec4(vec3(lum),255);
    gl_FragColor=v/255.0;
}
float getLum(vec3 color){
    return dot(color,vec3(0.2126,0.7162,0.0722));
}

参数限定词

我们通过参数限定词，可以更好的控制参数的行为。

参数的行为是围绕参数读写和拷贝考虑的。

我们通过参数的限定词来说一下参数行为：

in 参数深拷贝，可读写，不影响原始数据，默认限定词
1
2
3
4
5
6
7
8
9
10
precision mediump float;
void setColor(in vec3 color){
    color.x=0.0;
}
void main(){
    vec3 color=vec3(255);
    setColor(color);
    vec4 v=vec4(color,255);
    gl_FragColor=v/255.0;
}

在上面的主函数体中，我先声明了一个颜色color，我要通过setColor() 方法修改颜色。

当setColor() 方法中的形参color 被in 限定时，就相当于对实参进行了深拷贝，无论我在setColor() 方法里对color 做了什么，都不会影响原始的color 数据。

那么如果我想在setColor() 方法里修改原始的color数据，那就得使用out 限定。

out 参数浅拷贝，可读写，影响原始数据。
1
2
3
void setColor(out vec3 color){
    color.x=0.0;
}
const in 常量限定词，只读。
1
2
3
void setColor(const in vec3 color){
    color.x=0.0;
}

这样就是错误的
我们只能读取

1
2
3
void setColor(const in vec3 color){
    float r=color.r;
}

注：GLSL ES 还有许多内置方法，比如sin(),cos(),tan,atan() 等，建议大家去官方文档(https://registry.khronos.org/OpenGL-Refpages/es3/) 看一下。

变量的作用域

GLSL ES变量的作用域和es6 类似。

可以通过函数或{} 建立块级作用域，块级作用域内建立的变量就是局部变量。

局部变量只在块级作用域有效。

在函数之外建立的变量就是全局变量。

在代码块内可以直接获取其父级定义域的变量。

变量不存在“变量提升”现象，变量在使用时，需提前声明。

变量不能重复声明。

通过attribute、uniform、varying 限定字声明的变量都是全局变量。

const 可以声明常量，常量是只读的。

精度限定词

精度限定词可以提高着色程序的运行效率，削减内存开支。

精度的分类

webgl 提供了三种精度：

  • highp 高精度
  • mediump 中精度
  • lowp 低精度
    一般中精度用得会比较多，因为高精度太耗性能，而且有时候片元着色器会不支持，而低精度又太low。

精度的定义方法

我可以为某个变量设置精度，也可以为某种数据类型设置精度。

比如:

设置某个变量的精度：

1
2
3
mediump float size;
highp vec4 position;
lowp vec4 color;

设置某种数据类型的精度：

1
2
precision mediump float;
precision highp int;

注：

着色器中，除了片元着色器的float 数据没默认精度，其余的数据都是有默认精度的。

因此，我们在片元着色器里要提前声明好浮点型数据的精度。

结语

本篇文章就先到这里了，更多内容敬请期待，债见~

可视化学习 WebGL学习
上一篇:
【可视化学习】73-从入门到放弃WebGL(十)
下一篇:
前端读取excel文件内容导入table

    • blog of codesigner