微信小程序-EventChannel

前言

本篇将继续学习 WebGL。使用 WebGL 来实现一些效果

渐变的画布

这个很简单就可以实现，我们按照之前的 UV 逻辑就可进行实现

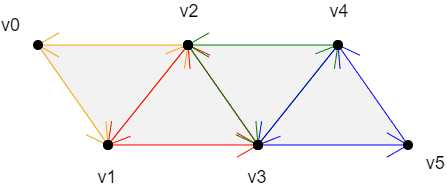
三角带的概念

首先我们将整个画布用一个颜色来进行绘制,这里因为用的三角带来进行绘制，所以点位是这样,逆时针绘制第一个三角形，第二个三角形以第一个三角形第二条边反向作为起始，逆时针绘制，差不多就是这样,其他的绘制方法，大家可以去考古我之前 webgl 的文章

上面四个面的绘制顺序是：

v0>v1>v2

以上一个三角形的第二条边+下一个点为基础，以和第二条边相反的方向绘制三角形

v2>v1>v3

以上一个三角形的第三条边+下一个点为基础，以和第三条边相反的方向绘制三角形

v2>v3>v4

以上一个三角形的第二条边+下一个点为基础，以和第二条边相反的方向绘制三角形

v4>v3>v5

规律：

第一个三角形：v0>v1>v2

第偶数个三角形：以上一个三角形的第二条边+下一个点为基础，以和第二条边相反的方向绘制三角形

第奇数个三角形：以上一个三角形的第三条边+下一个点为基础，以和第三条边相反的方向绘制三角形

代码

JS 代码

const source = new Float32Array([-1, 1, -1, -1, 1, 1, 1, -1]);

const rect = new Poly({
  gl,
  source,
  type: "TRIANGLE_STRIP",
  attributes: {
    a_Position: {
      size: 2,
      index: 0,
    },
  },
  uniforms: {
    u_CanvasSize: {
      type: "uniform2fv",
      value: [canvas.width, canvas.height],
    },
  },
});

顶点着色器

<!-- 顶点着色器 -->
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  void main(){
    gl_Position=a_Position;
  }
</script>

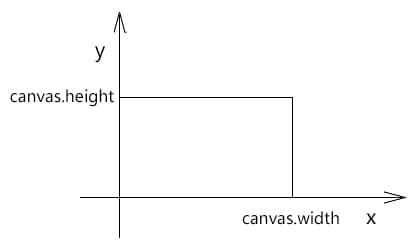
片元着色器

这里用了一个 gl_FragCoord 的 webgl 内置的 uv 参数，gl_FragCoord 是当前片元在 canvas 画布中的像素位，其坐标系和 canvas 画布的坐标系类似，其坐标基底的两个分量都是一个像素的宽和高。

只不过 FragCoord 坐标原点在左下角，y 轴朝上，效果如下：

<!-- 片元着色器 -->
<script id="fragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  uniform vec2 u_CanvasSize;
  void main(){
    gl_FragColor=vec4(
      gl_FragCoord.x/u_CanvasSize.x,
      gl_FragCoord.y/u_CanvasSize.y,
      0.8,
      1
    );
  }
</script>

那这样，我们就可以理解了，这里的渐变就是
左下角的 x 值是 0，y 也是 0，颜色就是 rgba(0,0,0.8,1),因为要转化成 255 的，所以颜色就这样(0,0,204,1)

左上角的 x 值是 0，y 是 1，颜色是 rgba(0,1,0.8,1)

右下角的 x 值是 1,y 是 0，颜色就是 rgba(1,0,0.8,1)

右上角的 x 值就是 1，y 值也是 1，颜色就是 rgba(1,1,0.8,1)

最终效果就是和我们想的是一样的

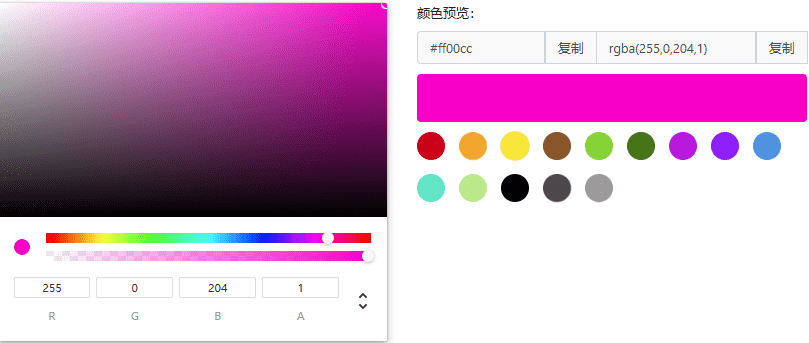
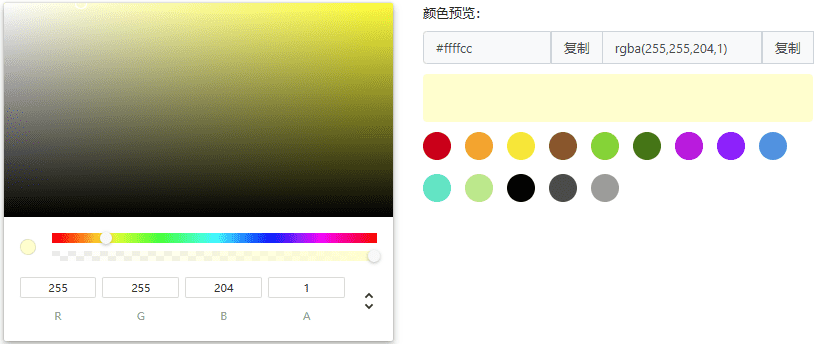
线性渐变对象

线性渐变对象具备一个起点、一个终点，用于限定渐变范围。

线性渐变对象中具备多个渐变节点，每个渐变节点都有以下属性：

节点颜色
节点位置 ，[0,1] 之间
我们这里简化一下，就给起点和终点位置设置两个颜色节点。

建立矩阵对象

const rect = new Poly({
    gl,
    source,
    type: 'TRIANGLE_STRIP',
    attributes: {
        a_Position: {
            size: 2,
            index: 0
        }
    },
    uniforms: {
        u_Start: {
            type: 'uniform2fv',
            value: [canvas.width * 0.25, canvas.height * 0.75]
        },
        u_End: {
            type: 'uniform2fv',
            value: [canvas.width * 0.75, canvas.height * 0.25]
        },
        u_Color0: {
            type: 'uniform4fv',
            value: [1, 0, 0, 1]
        },
        u_Color1: {
            type: 'uniform4fv',
            value: [1, 1, 0, 1]
        },
    }
})

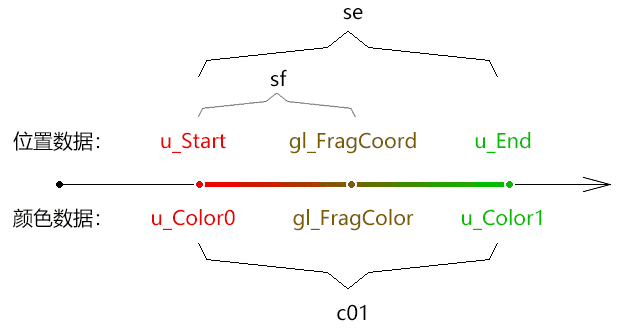
uniforms 中变量的意思：

• u_Start 起始点
• u_End 终点
• u_Color0 对应起点的颜色
• u_Color1 对应终点的颜色

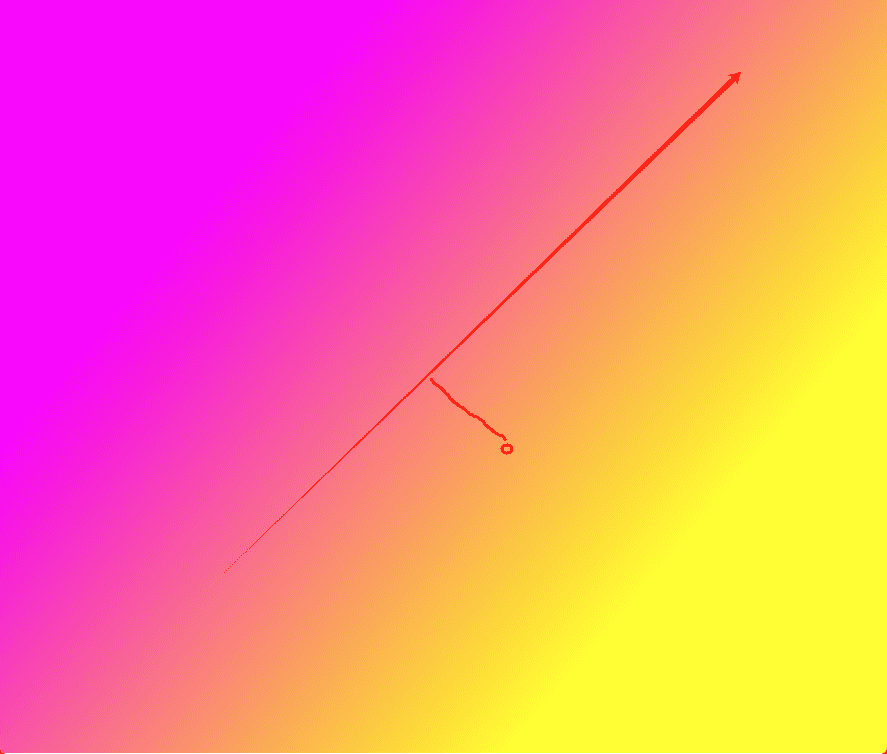
片元着色器

precision mediump float;

uniform vec4 u_Color0;
uniform vec4 u_Color1;
vec4 c01=u_Color1-u_Color0;

uniform vec2 u_Start;
uniform vec2 u_End;
vec2 se=u_End-u_Start;
float seLen=length(se);
vec2 normal=normalize(se);

void main(){
    vec2 sf=vec2(gl_FragCoord)-u_Start;
    float fsLen=clamp(dot(sf,normal),0.0,seLen);
    float ratio=fsLen/seLen;
    gl_FragColor=u_Color0+c01*ratio;
}

接下来我逐行解释一下这个代码

代码 1

precision mediump float;

设置浮点数精度为中等精度。

代码 2

uniform vec4 u_Color0;
uniform vec4 u_Color1;
vec4 c01 = u_Color1 - u_Color0;

定义两个颜色向量 u_Color0 和 u_Color1，并计算它们的差值 c01。

代码 3

uniform vec2 u_Start;
uniform vec2 u_End;
vec2 se = u_End - u_Start;
float seLen = length(se);
vec2 normal = normalize(se);

定义起点 u_Start 和终点 u_End，计算它们之间的向量 se、向量长度 seLen 和单位向量 normal。

代码 4

void main() {
    vec2 sf = vec2(gl_FragCoord) - u_Start;
    float fsLen = clamp(dot(sf, normal), 0.0, seLen);
    float ratio = fsLen / seLen;
    gl_FragColor = u_Color0 + c01 * ratio;
}

main() 函数是这段着色器程序的入口点，计算每个像素的颜色值。

sf 是当前像素位置与起点 u_Start 的向量。
fsLen 是 sf 在 normal 方向上的投影长度，使用 clamp 函数确保长度在 [0, seLen] 范围内。
ratio 是 fsLen 相对于总长度 seLen 的比例。
gl_FragColor 是最终的像素颜色，使用起点颜色 u_Color0 加上线性插值的颜色变化 c01 * ratio。

如果我们想要一个纵向的渐变，就只需要把起始点和结束点修改一下

 u_Start: {
    type: 'uniform2fv',
    // value: [canvas.width * 0.25, canvas.height * 0.75]
    value: [canvas.width * 0.4, 0]
},
u_End: {
    type: 'uniform2fv',
    // value: [canvas.width * 0.75, canvas.height * 0.25]
    value: [canvas.width * 0.6, 0]
},

多节点线性渐变

在上面的线性渐变的基础之上,我们可以实现多节点线性渐变

声明渐变的基础数据

//起始位
vec2 u_Start=vec2(100,100);
//结束位
vec2 u_End=vec2(700,700);
//节点颜色集合
vec4 colors[3];
//节点位置集合
float ratios[3];

基于渐变起点和结束点计算向量、向量长度和单位向量。

//终点减起点向量
vec2 se=u_End-u_Start;
//长度
float seLen=length(se);
//单位向量
vec2 se1=normalize(se);

在main函数体中填充颜色集合和节点位置集合，然后获取片元颜色。

void main(){
    colors[0]=vec4(1,0,0,1);
    colors[1]=vec4(1,1,0,1);
    colors[2]=vec4(0,1,0,1);
    ratios[0]=0.0;
    ratios[1]=0.5;
    ratios[2]=1.0;
    gl_FragColor=getColor(colors,ratios);
}

建立基于节点颜色集合和节点位置集合获取颜色的方法。

//获取片元颜色
vec4 getColor(vec4 colors[3],float ratios[3]){
    //片元颜色
    vec4 color=vec4(1);
    //当前片元减起始片元的向量
    vec2 sf=vec2(gl_FragCoord)-u_Start;
    //当前片元在se上的投影长度
    float fsLen=clamp(dot(sf,se1),0.0,seLen);
    //长度比
    float ratio=clamp(fsLen/seLen,ratios[0],ratios[3-1]);
    //第一个比值
    float ratio1=ratios[0];
    //第一个颜色
    vec4 color1=colors[0];
    //遍历节点，按比值取色
    for(int i=1;i<3;i++){
        //第二个比值
        float ratio2=ratios[i];
        //第二个颜色
        vec4 color2=colors[i];
        if(ratio>=ratio1&&ratio<=ratio2){
            //一段颜色的差值
            vec4 color2_1=color2-color1;
            //当前比值在一段比值中的比值
            float ratioInRatio=(ratio-ratio1)/(ratio2-ratio1);
            //当前比值在当前颜色段中所对应的颜色
            color=color1+color2_1*ratioInRatio;
            break;
        }
        ratio1=ratio2;
        color1=color2;
    }
    return color;
}

这里其实就是判断那个比值是在那部分的，因为我们有3个点，等于是2段线段，然后根据比值，可以得到是在哪一段线段上,也就是。

ratio>=ratio1&&ratio<=ratio2

然后里面的代码颜色变化就是按照那一段线段相减

//一段颜色的差值
vec4 color2_1=color2-color1;

然后就是下面这段代码的理解了

(ratio-ratio1)/(ratio2-ratio1);

首先我们要知道，这里的ratio1，和ratio2不是固定的，我们以比例在0.4，0.8举例说明,当ratio是0.4长度的时候，说明此时的ratio1是0,ratio2是0.5,此时我们计算出来，(0.4-0)/(0.6-0.4)=0.8,符合我们的设想(0.4/0.5=0.8),假设我们的ratio是0.8，那么此时的ratio1是0.5，ratio2是1，此时我们计算出来的值(0.8-0.5)/(1-0.5)=0.6,符合我们的设想(0.3/0.5=0.6)

完整代码

<!-- 片元着色器 -->
<script id="fragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  uniform vec2 u_CanvasSize;
  //起始位
  vec2 u_Start=vec2(100,100);
  //结束位
  vec2 u_End=vec2(700,700);
  //节点颜色集合
  vec4 colors[3];
  //节点位置集合
  float ratios[3];

  //终点减起点向量
  vec2 se=u_End-u_Start;
  //长度
  float seLen=length(se);
  //单位向量
  vec2 se1=normalize(se);

  //获取片元颜色
  vec4 getColor(vec4 colors[3],float ratios[3]){
      //片元颜色
      vec4 color=vec4(1);
      //当前片元减起始片元的向量
      vec2 sf=vec2(gl_FragCoord)-u_Start;
      //当前片元在se上的投影长度
      float fsLen=clamp(dot(sf,se1),0.0,seLen);
      //长度比
      float ratio=clamp(fsLen/seLen,ratios[0],ratios[3-1]);
      //第一个比值
      float ratio1=ratios[0];
      //第一个颜色
      vec4 color1=colors[0];
      //遍历节点，按比值取色
      for(int i=1;i<3;i++){
          //第二个比值
          float ratio2=ratios[i];
          //第二个颜色
          vec4 color2=colors[i];
          if(ratio>=ratio1&&ratio<=ratio2){
              //一段颜色的差值
              vec4 color2_1=color2-color1;
              //当前比值在一段比值中的比值
              float ratioInRatio=(ratio-ratio1)/(ratio2-ratio1);
              //当前比值在当前颜色段中所对应的颜色
              color=color1+color2_1*ratioInRatio;
              break;
          }
          ratio1=ratio2;
          color1=color2;
      }
      return color;
  }

  void main(){
    colors[0]=vec4(1,0,0,1);
    colors[1]=vec4(1,1,0,1);
    colors[2]=vec4(0,1,0,1);
    ratios[0]=0.0;
    ratios[1]=0.5;
    ratios[2]=1.0;
    gl_FragColor=getColor(colors,ratios);
  }
</script>

用js向片元着色器传递渐变数据

上面的多节点线性渐变，我是代码写死的，接下来用js将值进行传递

js只能向着色器传递有限类型的数据，它无法传递任意长度的数组、字符串、json对象等。

比如无法传递任意长度的数组、字符串、json对象等。

所以我就把渐变节点装进了一个四维矩阵中，从而拼8个渐变节点出来，这对于一般的渐变操作是够的。

[
    123000120, 255000,
    255000000, 255077,
    255255000, 255128,
    255000, 255178,
    200, 255255,
    -1, -1,
    -1, -1,
    -1, -1
]
[
    123000120, 255000, 255000000, 255077,
    255255000, 255128, 255000, 255178,
    200, 255255,       -1, -1,
    -1, -1,            -1, -1
]

每两个数字构成一个渐变节点

如：123000120, 255000

第一列对应颜色节点的rgb数据

如：123000120 对应的rgb数据分别是123,0,120

第二列对应颜色节点的a数据和位置数据

如：255000 对应的a值是255，节点位置为0

接下来咱们看一下代码实现。

在矩形面中写入节点数据 u_ColorStops

const rect = new Poly({
    gl,
    source,
    type: 'TRIANGLE_STRIP',
    attributes: {
        a_Position: {
            size: 2,
            index: 0
        }
    },
    uniforms: {
        u_Start: {
            type: 'uniform2fv',
            value: [0, 0]
        },
        u_End: {
            type: 'uniform2fv',
            value: [canvas.width, canvas.height]
        },
        u_ColorStops: {
            type: 'uniformMatrix4fv',
            value: [
                123000120, 255000,
                255000000, 255077,
                255255000, 255128,
                255000, 255178,
                200, 255255,
                -1, -1,
                -1, -1,
                -1, -1
            ]
        }
    }
})

在片元着色器中写入相应的uniform变量

//起始位
uniform vec2 u_Start;
//结束位
uniform vec2 u_End;
//四阶矩阵
uniform mat4 u_ColorStops;
//终点减起点向量
vec2 se=u_End-u_Start;
//长度
float seLen=length(se);
//单位向量
vec2 se1=normalize(se);

在main函数内，声明节点的颜色集合和位置集合。

通过setColorStops()方法将u_ColorStops 中的数据解析入节点颜色集合和位置集合。

通过getColor()方法获取片元颜色。

void main(){
    //节点颜色集合
    vec4 colors[8];
    //节点位置集合
    float ratios[8];
    //基于四维矩阵解析节点集合
    setColorStops(colors,ratios);
    //片元颜色
    gl_FragColor=getColor(colors,ratios);
}

setColorStops() 将u_ColorStops 中的数据解析入节点颜色集合和位置集合。

void setColorStops(out vec4 colors[8],out float ratios[8]){
    //节点颜色数据
    vec4 colorSource=vec4(1);
    //节点位置数据
    float ratioSource=1.0;
    //遍历四维矩阵的
    for (int y=0;y<4;y++){
        for (int x=0;x<2;x++){
            int rgb=int(u_ColorStops[y][x*2]);
            int ar=int(u_ColorStops[y][x*2+1]);
            if(rgb>0){
                setColorStop(rgb,ar,colorSource,ratioSource);
            }
            colors[y*2+x]=colorSource;
            ratios[y*2+x]=ratioSource;
        }
    }
}

setColorStop() 解析节点数据

void setColorStop(int rgb,int ar,out vec4 color,out float ratio){
    int rc=rgb/1000000;
    int gc=(rgb-rc*1000000)/1000;
    int bc=rgb-int(rgb/1000)*1000;
    int ac=ar/1000;
    int ratioI=ar-ac*1000;
    color=vec4(float(rc),float(gc),float(bc),float(ac))/255.0;
    ratio=float(ratioI)/255.0;
}

getColor() 方法和之前一样。

优化js 中的节点数据

若我们觉得之前节点数据的书写方式不方便，也可以换成键值对的书写方式，然后对其进行解析。

const colorStops = [
    {
        color: [123, 0, 123, 255],
        stop: 0
    },
    {
        color: [255, 0, 0, 255],
        stop: 0.3
    },
    {
        color: [255, 255, 0, 255],
        stop: 0.5
    },
    {
        color: [0, 255, 0, 255],
        stop: 0.7
    },
    {
        color: [0, 0, 200, 255],
        stop: 1
    },
]

function parseColorStops(source) {
    const stops = new Array(16).fill(-1);
    source.forEach(({ color, stop }, stopInd) => {
        let rgb = '';
        let ar = '';
        color.forEach((ele, ind) => {
            const str = (ele + 1000).toString().slice(1);
            if (ind < 3) {
                rgb += str;
            } else {
                ar += str;
            }
        })
        ar += (Math.round(stop * 255) + 1000).toString().slice(1);
        stops[stopInd * 2] = rgb;
        stops[stopInd * 2 + 1] = ar;
    })
    return stops;
}

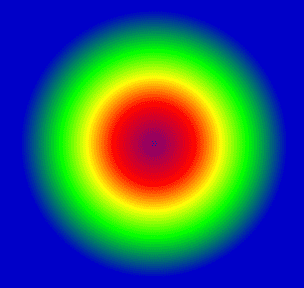
径向渐变

我们简单修改下之前的代码

在矩形面中，注释终点，添加半径

// u_End: {
//   type: 'uniform2fv',
//   value: [canvas.width, canvas.height]
// },
u_Radius: {
    type: 'uniform1f',
    value: 400
},

在片元着色器中也做相应调整。

//起始位
uniform vec2 u_Start;
//结束位
//uniform vec2 u_End;
//半径
uniform float u_Radius;
//四阶矩阵
uniform mat4 u_ColorStops;
//终点减起点向量
//vec2 se=u_End-u_Start;
//长度
//float seLen=length(se);
//单位向量
//vec2 se1=normalize(se);

修改获取片元颜色的方法，基于极径取ratio比值。

//获取片元颜色
vec4 getColor(vec4 colors[8],float ratios[8]){
    //片元颜色
    vec4 color=vec4(1);
    //当前片元减起始片元的向量
    //vec2 sf=vec2(gl_FragCoord)-u_Start;
    //当前片元到起始点的距离
    float fsLen=distance(gl_FragCoord.xy,u_Start);
    //当前片元在se上的投影长度
    //float fsLen=clamp(dot(sf,se1),0.0,seLen);
    //极径比
    float ratio=clamp(fsLen/u_Radius,ratios[0],ratios[8-1]);
    ……
}

极坐标渐变

我们将之前的代码改改，还可以实现极坐标渐变。

在矩形面中，注释终点

// u_End: {
//   type: 'uniform2fv',
//   value: [canvas.width, canvas.height]
// },

在片元着色器中也做相应调整。

//起始位
uniform vec2 u_Start;
//结束位
//uniform vec2 u_End;
//终点减起点向量
//vec2 se=u_End-u_Start;
//四阶矩阵
uniform mat4 u_ColorStops;
//长度
//float seLen=length(se);
//单位向量
//vec2 se1=normalize(se);
//一圈的弧度
float pi2=radians(360.0);

修改获取片元颜色的方法，基于极角取ratio比值。

这里因为dir可能是负的，所以加个π*2

//获取片元颜色
vec4 getColor(vec4 colors[8],float ratios[8]){
    //片元颜色
    vec4 color=vec4(1);
    //当前片元减起始片元的向量
    vec2 sf=vec2(gl_FragCoord)-u_Start;
    //当前片元在se上的投影长度
    //float fsLen=clamp(dot(sf,se1),0.0,seLen);
    //长度比
    //float ratio=clamp(fsLen/seLen,ratios[0],ratios[8-1]);
    //向量方向
    float dir=atan(sf.y,sf.x);
    if(dir<0.0){
        dir+=pi2;
    }
    float ratio=dir/pi2;
    ……
}

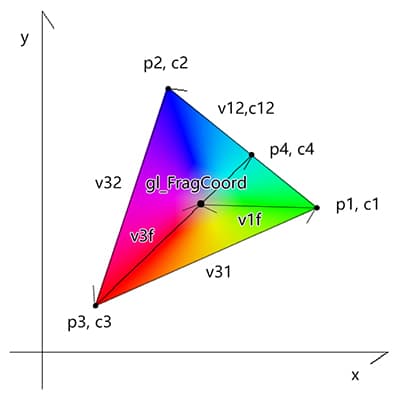
三点渐变

通过径向渐变和极坐标渐变的原理，还可以实现三点渐变。

建立三个点

//点1
vec2 p1=vec2(200,200);
vec4 c1=vec4(1,0,0,1);
//点2
vec2 p2=vec2(800,400);
vec4 c2=vec4(0,1,0,1);
//点3
vec2 p3=vec2(400,800);
vec4 c3=vec4(0,0,1,1);

p1是点位，c1是颜色。

基于三个位置点计算相应向量

vec2 v31=p1-p3;
vec2 v32=p2-p3;
vec2 v12=p2-p1;

提前算出p2和p1点位的色差

vec4 c12=c2-c1;

提前算出一圈的弧度，以备后用

float pi2=radians(360.0);

radians() 是将角度转弧度的方法，360°=π*2

建立基于向量获取弧度的方法

float getAngle(vec2 v){
    float ang=atan(v.y,v.x);
    if(ang<0.0){
        ang+=pi2;
    }
    return ang;
}

atan() 方法可以计算一个点基于x轴正方向的弧度，此弧度的取值范围是[-π,π]，为了方便计算，我将其范围设置为[0,2π]

获取点p1、p2和当前片元位相对于p3点的弧度。

float ang31=getAngle(v31);
float ang32=getAngle(v32);
vec2 v3f=gl_FragCoord.xy-p3;
float ang3f=getAngle(v3f);

用叉乘计算当前片元在向量v12的哪一侧

小于0，左侧，大于0，右侧，等于0重合。

vec2 v1f=gl_FragCoord.xy-p1;
float z=v1f.x*v12.y-v1f.y*v12.x;

这里可以使用webgl自带的cross来实现

float z =cross(vec3(v1f,0),vec3(v12,0)).z;

当片元在向量v31和v32之间，并且当前片元在向量v12的左侧时，当前片元在△p1p2p3中，我们便可以计算片元颜色。

vec4 color=vec4(0);
if(ang3f>=ang31&&ang3f<=ang32&&z<0.0){
    //计算∠<v3f,p3p1>在∠<p3p2,p3p1>中的比值
    ang3f=clamp(ang3f,ang31,ang32);
    float angRatio=(ang3f-ang31)/(ang32-ang31);

    //向量v12和向量v3f的交点位置和颜色
    vec2 p4=p1+v12*angRatio;
    vec4 c4=c1+c12*angRatio;

    //向量p3-gl_FragCoord在向量p3p4中的长度比
    float lenE=distance(p4,p3);
    float lenF=length(v3f);
    float lenRatio=lenF/lenE;

    //基于长度比获取当前片元在c3、c4间的颜色
    color=c3+(c4-c3)*lenRatio;
}
//片元颜色
gl_FragColor=color;

解释一下if语法中的取色逻辑。

计算∠<v32,v3f>在∠<v32,v31>中的比值angRatio

ang3f=clamp(ang3f,ang31,ang32);
float angRatio=(ang3f-ang31)/(ang32-ang31);

基于angRatio计算向量v12和向量v1f的交点位置p4和颜色c4

vec2 p4=p1+v12*angRatio;
vec4 c4=c1+c12*angRatio;

计算向量p3-gl_FragCoord在向量p3p4中的长度比，然后基于此比值获取当前片元在c3、c4间的颜色

float lenE=distance(p4,p3);
float lenF=length(v3f);
float lenRatio=lenF/lenE;
color=c3+(c4-c3)*lenRatio;

杂色

杂色的真谛就是通过有规律条件得到无规律的结果。

有规律的条件，是片元在canvas画布中的像素位。

无规律的结果，是片元的随机色值。

杂色的实现思路很简单，方法也非常多。

接下来我们就写一个杂色的实现方法。

在片元着色器里建立一个基于gl_FragCoord 获取随机颜色的方法。

float rand(vec2 fragCoord){
    vec2 a= vec2(0.1234,0.5678);
    float n= dot(fragCoord,a);
    return fract(sin(n)*10000.0);
}
//sin(n)∈[-1,1]
//sin(n)=-0.12345678
//sin(n)*10000.0=1234.5678
//fract(sin(n)*10000.0)=0.5678 ∈(0,1)

向量a 是随便写的一个向量，小数点后的位数要多一点。

n是片元位置与向量a的点积，这么做是为了将两个已知条件，即fragCoord 的两个分量，合成一个已知条件。

tan(n) 是基于n值获取[-∞,∞] 之间一个随机数，是为了把片元位的行列规律破一下。

sin(n)*10000.0 是为了把小数点左移，之后通过fract() 只获取小数点后面数字，这样的结果便会更为随机。

在主函数体中调用rand()方法

void main(){
    float f = rand(gl_FragCoord.xy);
    gl_FragColor = vec4(f, f, f, 1);
}

我们接下来对上面的向量a 进行旋转，可以实现噪波动画。

在片元着色器中添加u_Ang 变量：

<script id="fragmentShader" type="x-shader/x-fragment">
    precision mediump float;
    uniform float u_Ang;
    float s=sin(u_Ang);
    float c=cos(u_Ang);
    mat2 m=mat2(
      c,s,
      -s,c
    );
    float rand(vec2 fragCoord){
      vec2 a= m*vec2(0.1234,0.5678);
      float n= dot(fragCoord,a);
      return fract(tan(n)*10000.0);
    }
    void main(){
      float f = rand(gl_FragCoord.xy);
      gl_FragColor = vec4(f, f, f, 1);
    }
</script>

js代码

const rect = new Poly({
    gl,
    source,
    type: 'TRIANGLE_STRIP',
    attributes: {
        a_Position: {
            size: 2,
            index: 0
        }
    },
    uniforms: {
        u_Ang: {
            type: 'uniform1f',
            value: 0
        }
    }
})

let ang = 1;
!(function ani() {
    ang++;
    rect.uniforms.u_Ang.value = ang;
    rect.updateUniform()
    gl.clear(gl.COLOR_BUFFER_BIT);
    rect.draw()
    requestAnimationFrame(ani)
})()

肌理

肌理是美学中必不可少的一部分，不同的肌理有着不同的视觉体验。

我们可以把之前的代码做一下修改。

把10000.0变成10.0

vec2 a= vec2(0.1234,0.5678);
float n= dot(fragCoord,a);
return fract(tan(n)*10.0);

有韵律的杂色。

或者直接把10.0 也去掉

vec2 a= vec2(0.1234,0.5678);
float n= dot(fragCoord,a);
return fract(tan(n));

把a改一下

vec2 a= vec2(0.111,0.11);
float n= dot(fragCoord,a);
return fract(tan(n));

再把a改一下

vec2 a= vec2(0.111,0.111);
float n= dot(fragCoord,a);
return fract(tan(n));

或者还可以这样

float rand(vec2 fragCoord){
    vec2 v=fragCoord-u_CanvasSize/2.0;
    return fract(
        atan(v.x,v.y)*500.0
    );
}

结语

本篇文章就到这里了，更多内容敬请期待，债见~