【可视化学习】82-从入门到放弃WebGL(十四)
发表于：2024-08-21 |

前言

本篇文章继续跟着李伟老师学习WebGL，本篇主要来学习正交投影矩阵和视图矩阵。

正交投影矩阵

WebGL 是一个光栅引擎，其本身并不会实现三维效果，那我们要在其中实现三维效果的关键就在于算法：
顶点在裁剪空间中的位置=投影矩阵*视图矩阵*模型矩阵*顶点的初始点位

正交投影矩阵是投影矩阵的一种，我们先从它说起。

在说正交投影矩阵之前，我们还需要对裁剪空间有一个清晰的认知。

裁剪空间

裁剪空间是用于显示webgl图形的空间，此空间是一个宽、高、深皆为2 的盒子。其坐标系的原点在canvas画布的中心，如下图：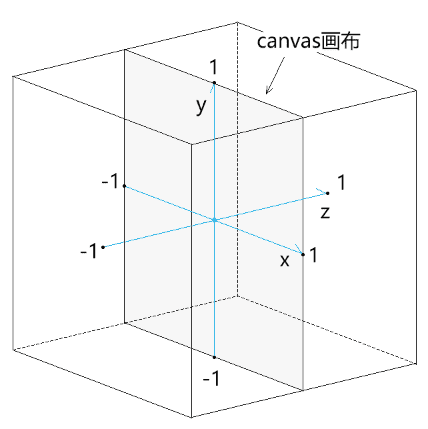
裁剪空间
裁剪空间中：

  • x轴上-1的位置对应canvas画布的左边界，1的位置对应canvas 画布的右边界
  • y轴上-1的位置对应canvas画布的下边界，1的位置对应canvas 画布的上边界
  • z轴上-1的位置朝向屏幕外部，1的位置朝向屏幕内部，如下图：
    裁剪空间

正交投影矩阵的实现原理

正交投影矩阵
正交投影矩阵 orthographic projection：将世界坐标系中的一块矩形区域(正交相机的可视区域)投射到裁剪空间中，不同深度的物体不具备近大远小的透视规则。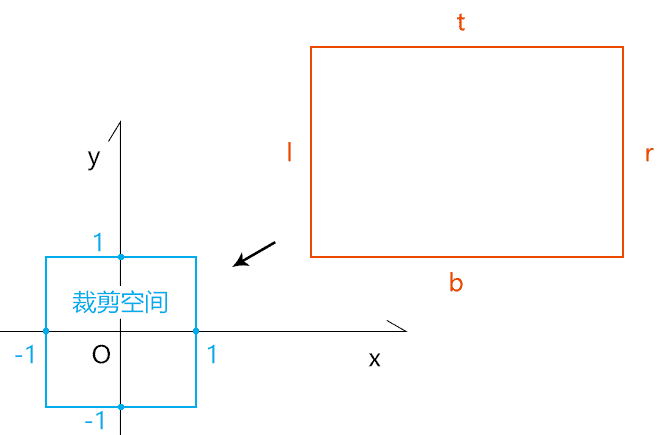
正交投影矩阵
接下来我们试想一下，如何将这个立方体放入裁剪空间中，很明显就是分成俩步，先位移再缩放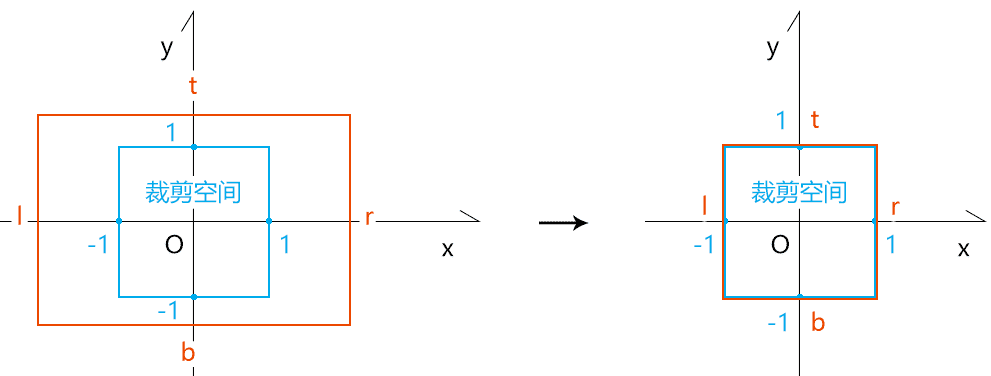
裁剪空间分步

设：正交相机可视区域的上、下、左、右、前、后的边界分别是t、b、l、r、n、f

  1. 位移矩阵
    1
    2
    3
    4
    5
    6
    [
        1,0,0,-(r+l)/2,
        0,1,0,-(t+b)/2,
        0,0,1,-(f+n)/2,
        0,0,0,1,
    ]
    位移矩阵
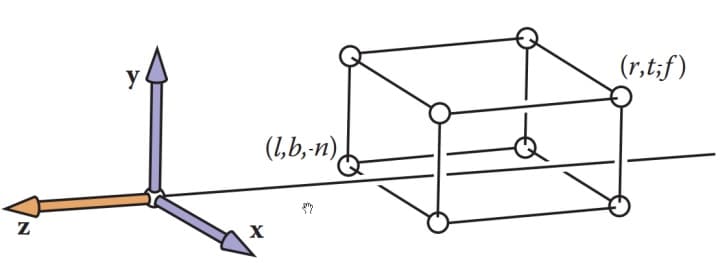
    我们根据这个图，要将后面的长方体的中心点放置到坐标系的原点，就可以轻松得到这个位移矩阵，往x轴移动-(r+l)/2,y轴移动-(t+b)/2,z轴移动-(f+n)/2
  2. 缩放矩阵
    1
    2
    3
    4
    5
    6
    [
        2/(r-l), 0,       0,        0,
        0,       2/(t-b), 0,        0,
        0,       0,       2/(f-n), 0,
        0,       0,       0,        1,
    ]
    然后可以根据图得到缩放矩阵,最后的x，y，z的距离都是1 - (-1)=2,而之前长方体的距离分别为(r-l),(t-b),(f-n)
    这样就可以得到我们需要的正交投影矩阵
  3. 正交投影矩阵=缩放矩阵*位移矩阵
    1
    2
    3
    4
    5
    6
    [
        2/(r-l), 0,       0,        -(r+l)/(r-l),
        0,       2/(t-b), 0,        -(t+b)/(t-b),
        0,       0,       2/(f-n),  -(f+n)/(f-n),
        0,       0,       0,        1,
    ]
    n、f是一个距离量，而不是在z轴上的刻度值，正交投影矩阵在z轴上的缩放因子需要取反,这个也容易理解，因为我们z轴是朝着我们自己的，f是距离离我们比较远的点，所以就可以得到最终的正交投影矩阵为以下公式。
    1
    2
    3
    4
    5
    6
    [
        2/(r-l), 0,       0,         -(r+l)/(r-l),
        0,       2/(t-b), 0,         -(t+b)/(t-b),
        0,       0,       -2/(f-n),  -(f+n)/(f-n),
        0,       0,       0,         1,
    ]

正交投影矩阵的代码实现

正交投影矩阵的代码实现很简单，我们可以直接从three.js 的Matrix4对象的makeOrthographic() 方法中找到，这个和我们上面推导出来的公式是一样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
makeOrthographic( left, right, top, bottom, near, far ) {

    const te = this.elements;
    const w = 1.0 / ( right - left );
    const h = 1.0 / ( top - bottom );
    const p = 1.0 / ( far - near );

    const x = ( right + left ) * w;
    const y = ( top + bottom ) * h;
    const z = ( far + near ) * p;

    te[ 0 ] = 2 * w;    te[ 4 ] = 0;    te[ 8 ] = 0;    te[ 12 ] = - x;
    te[ 1 ] = 0;    te[ 5 ] = 2 * h;    te[ 9 ] = 0;    te[ 13 ] = - y;
    te[ 2 ] = 0;    te[ 6 ] = 0;    te[ 10 ] = - 2 * p;    te[ 14 ] = - z;
    te[ 3 ] = 0;    te[ 7 ] = 0;    te[ 11 ] = 0;    te[ 15 ] = 1;

    return this;
}

以前我们在绘制webgl 图形的时候，它们会随canvas 画布的大小发生拉伸，对于这个问题，我们便可以用投影矩阵来解决。

使用正交投影矩阵解决webgl图形拉伸问题

我们拿之前三角形绘制的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
<body>
  <canvas id="canvas"></canvas>
  <!-- 顶点着色器 -->
  <script id="vertexShader" type="x-shader/x-vertex">
      attribute vec4 a_Position;
      void main(){
        gl_Position = a_Position;
      }
  </script>
  <!-- 片元着色器 -->
  <script id="fragmentShader" type="x-shader/x-fragment">
      precision mediump float;
      uniform vec4 u_Color;
      void main(){
        gl_FragColor=u_Color;
      }
  </script>
  <script type="module">
    import { initShaders } from '../jsm/Utils.js';
    import Poly from './jsm/Poly.js'

    const canvas = document.getElementById('canvas');
    const [viewW, viewH] = [window.innerWidth, window.innerHeight]
    canvas.width = viewW;
    canvas.height = viewH;
    const gl = canvas.getContext('webgl');

    const vsSource = document.getElementById('vertexShader').innerText;
    const fsSource = document.getElementById('fragmentShader').innerText;
    initShaders(gl, vsSource, fsSource);
    gl.clearColor(0.0, 0.0, 0.0, 1.0);


    const triangle = new Poly({
      gl,
      source: [
        0, 0.3, -0.2,
        - 0.3, -0.3, -0.2,
        0.3, -0.3, -0.2
      ],
      type: 'TRIANGLES',
      attributes: {
        a_Position: {
          size: 3,
          index: 0
        },
      },
      uniforms: {
        u_Color: {
          type: 'uniform4fv',
          value: [1, 1, 0, 1]
        },
      }
    })

    render()

    function render() {
      gl.clear(gl.COLOR_BUFFER_BIT);
      triangle.draw()
    }
  </script>
</body>

效果图

此时我们加上正交投影矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
<body>
  <canvas id="canvas"></canvas>
  <!-- 顶点着色器 -->
  <script id="vertexShader" type="x-shader/x-vertex">
      attribute vec4 a_Position;
      uniform mat4 u_ProjectionMatrix;
      void main(){
        gl_Position = u_ProjectionMatrix*a_Position;
      }
  </script>
  <!-- 片元着色器 -->
  <script id="fragmentShader" type="x-shader/x-fragment">
      precision mediump float;
      uniform vec4 u_Color;
      void main(){
        gl_FragColor=u_Color;
      }
  </script>
  <script type="module">
    import { initShaders } from '../jsm/Utils.js';
    import { Matrix4,  } from 'https://unpkg.com/three/build/three.module.js';
    import Poly from './jsm/Poly.js'

    const canvas = document.getElementById('canvas');
    const [viewW, viewH] = [window.innerWidth, window.innerHeight]
    canvas.width = viewW;
    canvas.height = viewH;
    const gl = canvas.getContext('webgl');

    const vsSource = document.getElementById('vertexShader').innerText;
    const fsSource = document.getElementById('fragmentShader').innerText;
    initShaders(gl, vsSource, fsSource);
    gl.clearColor(0.0, 0.0, 0.0, 1.0);

    //正交投影矩阵
    const projectionMatrix = new Matrix4()
    //定义相机世界高度尺寸的一半
    const halfH = 2
    //计算画布的宽高比
    const ratio = canvas.width / canvas.height
    //基于halfH和画布宽高比计算相机世界宽度尺寸的一半
    const halfW = halfH * ratio
    //定义相机世界的6个边界
    const [left, right, top, bottom, near, far] = [
      -halfW, halfW, halfH, -halfH, 0, 4
    ]
    //获取正交投影矩阵
    projectionMatrix.makeOrthographic(left, right, top, bottom, near, far)


    const triangle = new Poly({
      gl,
      source: [
        0, 0.3, -0.2,
        - 0.3, -0.3, -0.2,
        0.3, -0.3, -0.2
      ],
      type: 'TRIANGLES',
      attributes: {
        a_Position: {
          size: 3,
          index: 0
        },
      },
      uniforms: {
        u_Color: {
          type: 'uniform4fv',
          value: [1, 1, 0, 1]
        },
        u_ProjectionMatrix: {
          type: 'uniformMatrix4fv',
          value: projectionMatrix.elements
        },
      }
    })

    render()

    function render() {
      gl.clear(gl.COLOR_BUFFER_BIT);
      triangle.draw()
    }
  </script>
</body>

这时候就得到了一个没有被拉伸的三角形
效果图

逆矩阵

逆矩阵在图形项目的应用很广，所以咱们接下来就系统说一下逆矩阵的概念。

逆矩阵的概念

逆矩阵就好比咱们学习除法的时候，一个实数的倒数。

如：

2的倒数是1/2。

那么，矩阵m的倒数就是1/m。

只不过，1/m不叫做矩阵m的倒数，而是叫做矩阵m的逆矩阵。

由上，我们可以推导出的一些特性。

已知：

矩阵m
矩阵n
可得：

1.矩阵与其逆矩阵的相乘结果为单位矩阵

因为：

2*1/2=1

所以：

m*1/m=单位矩阵

2.矩阵m除以矩阵n就等于矩阵m乘以矩阵n的逆矩阵

因为：

3/2=3*1/2

所以：

m/n=m*1/n

矩阵转逆矩阵

位移矩阵的逆矩阵是取位移因子的相反数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const m=new Matrix4()
m.elements=[
  1,0,0,0,
  0,1,0,0,
  0,0,1,0,
  4,5,6,1,
]
console.log(m.invert().elements);
//打印结果
[
  1,0,0,0,
  0,1,0,0,
  0,0,1,0,
  -4,-5,-6,1,
]

缩放矩阵的逆矩阵是取缩放因子的倒数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
{
  const m=new Matrix4()
  m.elements=[
    2,0,0,0,
    0,4,0,0,
    0,0,8,0,
    0,0,0,1,
  ]
  console.log(m.invert().elements);
}
//打印结果
[
  0.5, 0, 0, 0, 
  0, 0.25, 0, 0,
  0, 0, 0.125, 
  0, 0, 0, 0, 1
]

3.旋转矩阵的逆矩阵是基于旋转弧度反向旋转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
{
  const ang=30*Math.PI/180
  const c=Math.cos(ang)
  const s=Math.sin(ang)
  const m=new Matrix4()
  m.elements=[
    c,s,0,0,
    -s,c,0,0,
    0,0,1,0,
    0,0,0,1,
  ]
  console.log(m.invert().elements);
}
//打印结果
[
  0.866, -0.45, 0, 0, 
  0.45, 0.866, 0, 0, 
  0, 0, 1, 0, 
  0, 0, 0, 1
]

视图矩阵

创建视图矩阵

我们之前已经说过了简单说过视图矩阵，这里使用视图矩阵结合投影矩阵做一个正交投影视图矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function getViewMatrix(e, t, u) {
  //基向量c，视线
  const c = new Vector3().subVectors(e, t).normalize()
  //基向量a，视线和上方向的垂线
  const a = new Vector3().crossVectors(u, c).normalize()
  //基向量b，修正上方向
  const b = new Vector3().crossVectors(c, a).normalize()
  //正交旋转矩阵
  const mr = new Matrix4().set(
    ...a, 0,
    ...b, 0,
    -c.x, -c.y, c.z, 0,
    0, 0, 0, 1
  )
  //位移矩阵
  const mt = new Matrix4().set(
    1, 0, 0, -e.x,
    0, 1, 0, -e.y,
    0, 0, 1, -e.z,
    0, 0, 0, 1
  )
  return mr.multiply(mt).elements
}

因为我们z轴是朝向我们的，所以正交旋转矩阵的z轴方向改一下。
然后创建我们的视点，上方向和，目标点

1
2
3
const eye = new Vector3(1, 0, 3);
const target = new Vector3(0.5, 0.5, 0);
const up = new Vector3(0, 1, 0);

这样我们的视图矩阵就创建好了

1
const viewMatrix=new Matrix4().fromArray(getViewMatrix(eye, target, up))
创建投影矩阵

然后我们根据上面学习的投影矩阵，创建正交投影矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const halfH = 2;
const ratio = canvas.width / canvas.height;
const halfW = halfH * ratio;
const [left, right, top, bottom, near, far] = [
    -halfW,
    halfW,
    halfH,
    -halfH,
    0,
    4,
];
//正交投影矩阵
const projectionMatrix = new Matrix4();
//获取正交投影矩阵
projectionMatrix.makeOrthographic(left, right, top, bottom, near, far);
结合投影和视图矩阵

接下来我们结合一下投影视图矩阵

1
2
3
4
5
// 投影视图矩阵
const pvMatrix = new Matrix4().multiplyMatrices(
    projectionMatrix,
    new Matrix4().fromArray(getViewMatrix(eye, target, up))
);
利用投影视图矩阵绘图

然后我们利用这个绘制一下俩个三角形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
<body>
    <canvas id="canvas"></canvas>
    <!-- 顶点着色器 -->
    <script id="vertexShader" type="x-shader/x-vertex">
      attribute vec4 a_Position;
      uniform mat4 u_PvMatrix;
      void main(){
        gl_Position = u_PvMatrix*a_Position;
      }
    </script>
    <!-- 片元着色器 -->
    <script id="fragmentShader" type="x-shader/x-fragment">
      precision mediump float;
      uniform vec4 u_Color;
      void main(){
        gl_FragColor=u_Color;
      }
    </script>
    <script type="module">
      import { initShaders } from "../jsm/Utils.js";
      import {
        Matrix4,
        Vector3,
      } from "https://unpkg.com/three/build/three.module.js";
      import Poly from "./jsm/Poly.js";

      const canvas = document.getElementById("canvas");
      const [viewW, viewH] = [window.innerWidth, window.innerHeight];
      canvas.width = viewW;
      canvas.height = viewH;
      const gl = canvas.getContext("webgl");

      const vsSource = document.getElementById("vertexShader").innerText;
      const fsSource = document.getElementById("fragmentShader").innerText;
      initShaders(gl, vsSource, fsSource);
      gl.clearColor(0.0, 0.0, 0.0, 1.0);

      const halfH = 2;
      const ratio = canvas.width / canvas.height;
      const halfW = halfH * ratio;
      const [left, right, top, bottom, near, far] = [
        -halfW,
        halfW,
        halfH,
        -halfH,
        0,
        4,
      ];
      const eye = new Vector3(1, 0, 3);
      const target = new Vector3(0.5, 0.5, 0);
      const up = new Vector3(0, 1, 0);

      //正交投影矩阵
      const projectionMatrix = new Matrix4();
      //获取正交投影矩阵
      projectionMatrix.makeOrthographic(left, right, top, bottom, near, far);

      // 视图矩阵
      function getViewMatrix(e, t, u) {
        //基向量c，视线
        const c = new Vector3().subVectors(e, t).normalize();
        //基向量a，视线和上方向的垂线
        const a = new Vector3().crossVectors(u, c).normalize();
        //基向量b，修正上方向
        const b = new Vector3().crossVectors(c, a).normalize();
        //正交旋转矩阵
        const mr = new Matrix4().set(
          ...a,0,
          ...b, 0,
          -c.x,-c.y,c.z,0,
          0,0,0,1
        );
        //位移矩阵
        const mt = new Matrix4().set(
          1,0,0,-e.x,
          0,1,0,-e.y,
          0,0,1,-e.z,
          0,0,0,1
        );
        return mr.multiply(mt).elements;
      }

      // 投影视图矩阵
      const pvMatrix = new Matrix4().multiplyMatrices(
        projectionMatrix,
        new Matrix4().fromArray(getViewMatrix(eye, target, up))
      );

      const triangle1 = crtTriangle(
        [1, 0, 0, 1],
        [0, 0.3, -0.2, -0.3, -0.3, -0.2, 0.3, -0.3, -0.2]
      );
      const triangle2 = crtTriangle(
        [1, 1, 0, 1],
        [0, 0.3, 0.2, -0.3, -0.3, 0.2, 0.3, -0.3, 0.2]
      );

      render();

      function render() {
        gl.clear(gl.COLOR_BUFFER_BIT);
        triangle1.init();
        triangle1.draw();
        triangle2.init();
        triangle2.draw();
      }

      function crtTriangle(color, source) {
        return new Poly({
          gl,
          source,
          type: "TRIANGLES",
          attributes: {
            a_Position: {
              size: 3,
              index: 0,
            },
          },
          uniforms: {
            u_Color: {
              type: "uniform4fv",
              value: color,
            },
            u_PvMatrix: {
              type: "uniformMatrix4fv",
              value: pvMatrix.elements,
            },
          },
        });
      }
    </script>
  </body>

正交投影视图矩阵

Threejs验证

然后我们可以用threejs来验证一下我们的写的正交投影矩阵

1
import { Matrix4, Vector3, OrthographicCamera } from 'https://unpkg.com/three/build/three.module.js';

这里我们导入了threejs的正交相机,然后将参数给正交相机得到正交投影视图矩阵，得到的效果图和我们之前的一样，这样我们也就顺便理解了lookAt的含义，也就是矩阵旋转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//正交相机
const camera = new OrthographicCamera(
    left, right, top, bottom, near, far
)
camera.position.copy(eye)
camera.lookAt(target)
camera.updateWorldMatrix(true)

//投影视图矩阵
const pvMatrix = new Matrix4()
    .multiplyMatrices(
    camera.projectionMatrix, // 正交投影矩阵
    camera.matrixWorldInverse // 视图矩阵
)

matrixWorldInverse是matrixWorld 的逆矩阵。也就是将本地坐标系转变成世界坐标系的逆矩阵，含义就是将世界坐标转化成物体坐标

分解lookAt步骤
  1. 由视点位置得出位移矩阵positionMatrix
    1
    const positionMatrix = new Matrix4().setPosition(eye)
  2. 由视点、目标点、上方向得出旋转矩阵rotationMatrix
    1
    const rotationMatrix = new Matrix4().lookAt(eye,target,up)
  3. 基于位移矩阵和旋转矩阵的逆矩阵(invert())计算视图矩阵 viewMatrix
    1
    2
    3
    4
    const viewMatrix = new Matrix4().multiplyMatrices(
        positionMatrix,
        rotationMatrix
    ).invert()

结语

本篇文章就到这里了，更多内容敬请期待，债见~

可视化学习 WebGL学习
上一篇:
【SVG学习】02-SVG动画
下一篇:
【英语学习】01-常用职场词汇

    • blog of codesigner