【可视化学习】83-从入门到放弃WebGL(十五)
发表于：2024-09-03 |

前言

本篇文章继续跟着李伟老师学习WebGL，本篇主要来学习透视投影矩阵

基础知识

在学习透视投影矩阵之前，需要补充回顾一些基础知识

齐次坐标系

在齐次坐标系中以下等式是成立的：

1
2
(x,y,z,1)=(x,y,z,1)*k=(kx,ky,kz,k) k≠0
(x,y,z,1)=(x,y,z,1)*z=(zx,zy,z²,z) z≠0

比如：
(1,0,0,1)和(2,0,0,2) 都代表同一个三维点位(1,0,0)

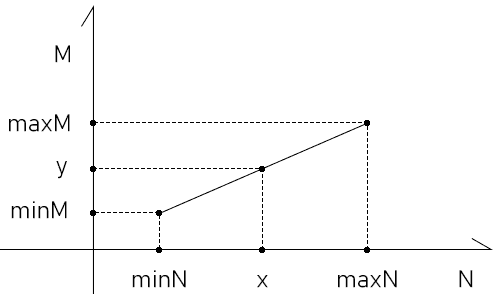
线性补间运算

之前我们说过斜截式y=kx+b，它就是线性补间运算的公式。

除了斜截式，两种数据间的线性映射关系还可以用其它方法来表示。
效果图

已知：
1.N类型的数据极值是[minN,maxN]

2.M类型的数据极值是[minM,maxM]

3.x属于N

4.将x映射到M的中的值为y

则x,y 的关系可以用两个等式表示：

比例式：
1
(x-minN)/(maxN-minN)=(y-minM)/(maxM-minM)
斜截式:
1
2
3
k=(maxM-minM)/(maxN-minN)
b=minM-minN*k
y=kx+b

通过线性插值的特性，我们可以知道：

[minN,maxN]中的每个点都与[minM,maxM]中的唯一点相对应，由一个x便可以求出唯一一个y。

基础知识咱们就先说到这，接下来咱们认识一下透视投影矩阵。

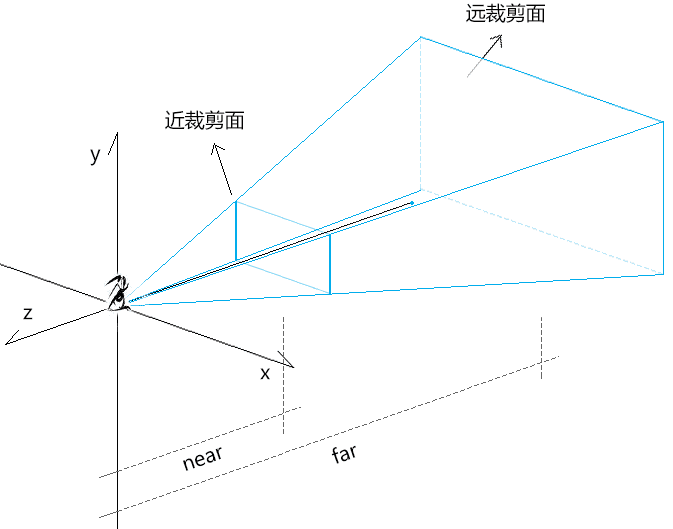
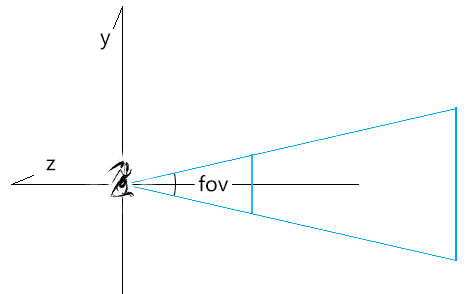
认识透视投影矩阵

透视投影矩阵 perspective projection：将世界坐标系中的一块四棱台形的区域投射到裁剪空间中，不同深度的物体具备近大远小的透视规则。
效果图
效果图

透视相机的建立需要以下已知条件：

  • fov：摄像机视锥体垂直视野角度
  • aspect：摄像机视锥体宽高比
  • near：摄像机近裁剪面到视点的距离
  • far：摄像机远裁剪面到视点的距离
    效果图

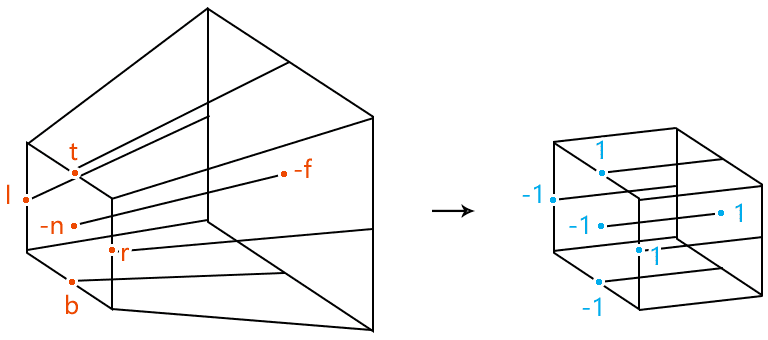
要将一个任意尺寸的正四棱台塞进裁剪空间里，分成2步

从透视到正交。
1.收缩远裁剪面，将原来的正四棱台变成长方体。
2.像之前的正交投影矩阵一样，将长方体先位移，再缩放。

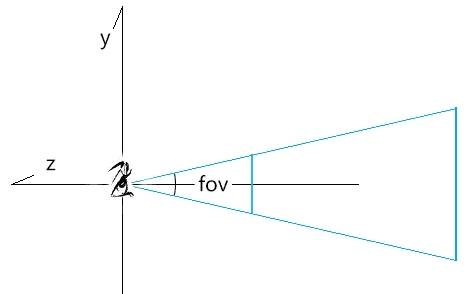
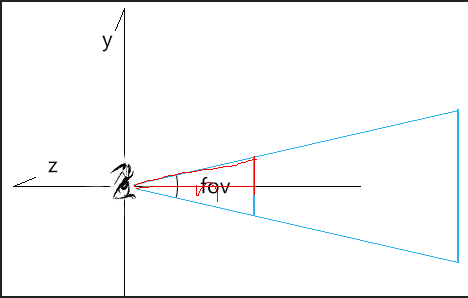
计算透视投影矩阵

基于fov、aspect、n(near)、f(far)计算近裁剪面边界。

效果图

1
2
3
4
t=n*tan(fov/2)
b=-t
r=t*aspect
l=-r

解释一下这段代码，根据之前的定义，我们已经知道了

  • fov：摄像机视锥体垂直视野角度
  • aspect：摄像机视锥体宽高比
  • near：摄像机近裁剪面到视点的距离
  • far：摄像机远裁剪面到视点的距离

那么近裁剪截面对应的y值就是n*tan(fov/2)就很好理解，我们看我画红线的三角形
效果图
这个三角形的角度就是fov/2,n * tan(fov/2)求出来的值就是这个三角形右侧上顶点的y值,也就是top,根据对应x轴对称，那么可以求得bottom的y值就是-t,然后因为aspect是摄像机视锥体的宽高比，高度是2t,那么宽度就是2t * aspect,根据对称关系，可以得到right为t * aspect,left为-t * aspect。

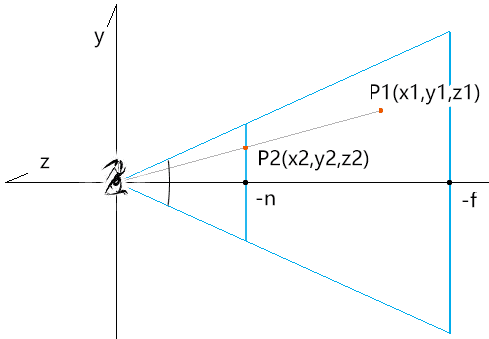
设：可视区域中一顶点为P1(x1,y1,z1)

求：求P1在近裁剪面上的投影P2(x2,y2,z2)
效果图
由相似三角形性质或者我们前面刚说过的直线的比例式得：

1
x1/x2=y1/y2=z1/z2

因为：

1
z2=-n

那么可得

1
2
x2=nx1/-z1
y2=ny1/-z1

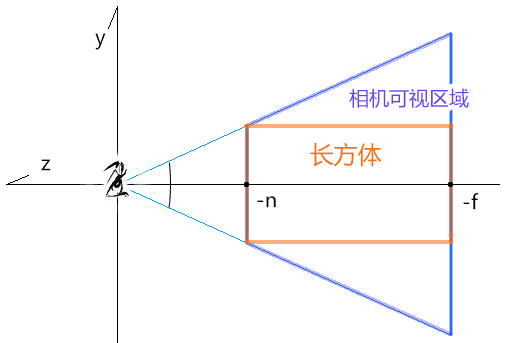
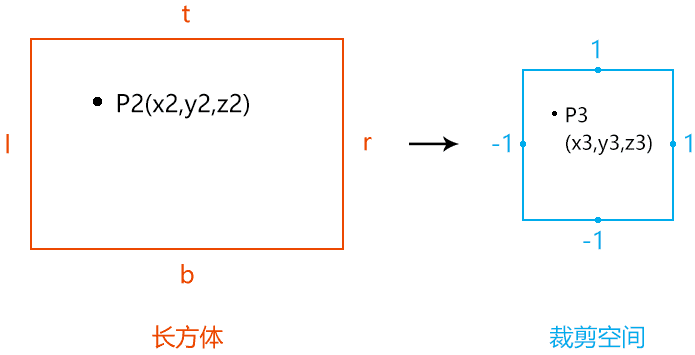
若我们把P1点的x1,y1替换成x2,y2，就可以理解为把相机可视区域塞进了一个长方体里。
效果图

把长方体里的顶点塞进裁剪空间中

效果图

在x方向可得
1
(x3-(-1))/(1-(-1))=(x2-l)/(r-l)

慢慢演算，可得到

1
x3=2x2/(r-l)-(r+l)/(r-l)

上面结果的具体演算如下:

1
2
3
4
5
6
7
(x3+1)/2=(x2-l)/(r-l)
(x3+1)=2(x2-l)/(r-l)
x3=2(x2-l)/(r-l)-1
x3=2(x2-l)/(r-l)-(r-l)/(r-l)
x3=(2(x2-l)-(r-l))/(r-l)
x3=(2x2-(r+l))/(r-l)
x3=2x2/(r-l)-(r+l)/(r-l)

然后我们将x2用x1替换掉,x2=nx1/-z1,得到公式

1
x3=(2n/(r-l))x1/-z1-(r+l)/(r-l)
在y方向可得
1
(y3-(-1))/(1-(-1))=(y2-b)/(t-b)

慢慢演算,可得到,或者根据x的结果可以模拟推断结果为(因为结构和上面的x是一样的)

1
y3=2y2/(t-b)-(t+b)/(t-b)

然后我们将y2用y1替换掉，y2=ny1/-z1，得到公式(因为结构和上面一样，所以还是可以类推)

1
y3=(2n/(t-b))y1/-z1-(t+b)/(t-b)
求透视投影矩阵

观察一下当前求出的x3,y3：

1
2
x3=(2n/(r-l))x1/-z1-(r+l)/(r-l)
y3=(2n/(t-b))y1/-z1-(t+b)/(t-b)

我们的公式非常的像，此时乘以一个-z1(因为y2=ny1/-z1,x2=nx2/-z1,所以用了-z1,你可以直接将结果带入前面的公式，就可以得到下面的公式),便可以得到一个齐次坐标P4(x4,y4,z4,w4)：

1
2
3
4
x4=(2n/(r-l))x1+((r+l)/(r-l))z1
y4=(2n/(t-b))y1+((t+b)/(t-b))z1
z4=?
w4=-z1

当前把顶点的z分量投射到裁剪空间中的方法，我们还不知道，所以z4=?

我们可以先从已知条件中提取投影矩阵(行主序)的矩阵因子：

1
2
3
4
5
6
[
  2n/(r-l)       0         (r+l)/(r-l)   0,
  0              2n/(t-b)  (t+b)/(t-b)   0,
  ?              ?          ?            ?,
  0              0          -1           0
]

接下来，就剩下z轴相关的矩阵因子了。

因为整个投影矩阵始终是在做线性变换的，投影点的z值与投影矩阵的z轴向的x,y分量无关。

所以投影矩阵的z轴向的x,y分量可以写做0，z和w分量可以设为k,b，如下：

1
2
3
4
5
6
[
  2n/(r-l)       0         (r+l)/(r-l)   0,
  0              2n/(t-b)  (t+b)/(t-b)   0,
  0              0          k            b
  0              0          -1           0
]

之前说了，整个投影矩阵始终是在做线性变换，所以我们可以用k,b组合一个斜截式：

1
z4=k*z1+b

当然，你也可以认为是点积的结果：

1
2
z4=(0,0,k,b)·(x1,y1,z1,1)
z4=k*z1+b

接下来，我们只要求出上面的k,b,就可以得到透视投影矩阵。

我们可以用当前的已知条件，构建一个二元一次方程组，求出k,b：
效果图
当z1=-n 时(近截面)，z3=-1，z4=-1*-z1 ，即：

1
2
3
4
z4=k*z1+b
-1*n=k*-n+b
-n=-kn+b
b=kn-n

当z1=-f时(远截面)，z3=1，z4=1*-z1，即：

1
2
3
4
5
z4=k*z1+b
1*f=k*-f+b
f=-kf+b
kf=b-f
k=(b-f)/f

用消元法求b：

1
2
3
4
5
6
7
8
b=kn-n
b=((b-f)/f)n-n
b=(b-f)n/f-n
fb=(b-f)n-fn
fb=bn-fn-fn
fb-bn=-2fn
b(f-n)=-2fn
b=-2fn/(f-n)

再求k：

1
2
3
4
5
6
k=(b-f)/f
k=(-2fn/(f-n)-f)/f
k=-2n/(f-n)-1
k=(-2n-f+n)/(f-n)
k=(-f-n)/(f-n)
k=-(f+n)/(f-n)

最终的透视投影矩阵如下：

1
2
3
4
5
6
[
  2n/(r-l)       0         (r+l)/(r-l)   0,
  0              2n/(t-b)  (t+b)/(t-b)   0,
  0              0         -(f+n)/(f-n)  -2fn/(f-n),
  0              0         -1            0
]

透视投影的建立方法，我们可以在three.js 的源码里找到。

three.js中的源码

大概如下,three.js 的PerspectiveCamera对象的updateProjectionMatrix() 方法，便是透视相机建立透视投影矩阵的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
updateProjectionMatrix() {
    const near = this.near;
      //近裁剪面上边界
    let top = near * Math.tan( MathUtils.DEG2RAD * 0.5 * this.fov ) / this.zoom;
    //近裁剪面高度
    let height = 2 * top;
    //近裁剪面宽度
    let width = this.aspect * height;
    //近裁剪面左边界
    let left = - 0.5 * width;
    //默认为null
    const view = this.view;

    //多视图
    if ( this.view !== null && this.view.enabled ) {
        const fullWidth = view.fullWidth,
              fullHeight = view.fullHeight;
        left += view.offsetX * width / fullWidth;
        top -= view.offsetY * height / fullHeight;
        width *= view.width / fullWidth;
        height *= view.height / fullHeight;

    }
    //偏离值，默认0
    const skew = this.filmOffset;
    if ( skew !== 0 ) left += near * skew / this.getFilmWidth();
    
    //基于近裁剪面边界、近裁剪面和远裁剪面到相机视点的距离设置投影矩阵
    this.projectionMatrix.makePerspective( left, left + width, top, top - height, near, this.far );

    //投影矩阵的逆矩阵
    this.projectionMatrixInverse.copy( this.projectionMatrix ).invert();

}

// makePerspective() 是Matrix4对象里的方法，会基于投影空间建立透视投影矩阵
makePerspective( left, right, top, bottom, near, far ) {
    const te = this.elements;
    
    const x = 2 * near / ( right - left );
    const y = 2 * near / ( top - bottom );
    const a = ( right + left ) / ( right - left );
    const b = ( top + bottom ) / ( top - bottom );
    const c = - ( far + near ) / ( far - near );
    const d = - 2 * far * near / ( far - near );

    te[ 0 ] = x;    te[ 4 ] = 0;    te[ 8 ] = a;    te[ 12 ] = 0;
    te[ 1 ] = 0;    te[ 5 ] = y;    te[ 9 ] = b;    te[ 13 ] = 0;
    te[ 2 ] = 0;    te[ 6 ] = 0;    te[ 10 ] = c;    te[ 14 ] = d;
    te[ 3 ] = 0;    te[ 7 ] = 0;    te[ 11 ] = - 1;    te[ 15 ] = 0;

    return this;
}

透视投影矩阵练习

我们已经计算出来了透视投影矩阵，接下来做个小练习

着色器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  uniform mat4 u_ProjectionMatrix;
  void main(){
      gl_Position = u_ProjectionMatrix*a_Position;
  }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  uniform vec4 u_Color;
  void main(){
      gl_FragColor=u_Color;
  }
</script>
初始化着色器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import { initShaders } from '../jsm/Utils.js';
import { Matrix4,PerspectiveCamera, Vector3, Quaternion, Object3D, OrthographicCamera } from 'https://unpkg.com/three/build/three.module.js';
import Poly from './jsm/Poly.js'

const canvas = document.getElementById('canvas');
const [viewW, viewH] = [window.innerWidth, window.innerHeight]
canvas.width = viewW;
canvas.height = viewH;
const gl = canvas.getContext('webgl');

const vsSource = document.getElementById('vertexShader').innerText;
const fsSource = document.getElementById('fragmentShader').innerText;
initShaders(gl, vsSource, fsSource);
gl.clearColor(0.0, 0.0, 0.0, 1.0);
建立透视相机
1
2
3
4
5
6
7
const [fov,aspect,near,far]=[
    45,
    canvas.width / canvas.height,
    1,
    20
]
const camera = new PerspectiveCamera(fov,aspect,near,far)
基于相机的透视投影矩阵，绘制4个三角形

前面是两个黄色三角形，后面是两个红色三角形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
const triangle1 = crtTriangle(
    [1, 0, 0, 1],
    [-0.5,0,-3]
)

const triangle2 = crtTriangle(
    [1, 0, 0, 1],
    [0.5,0,-3]
)

const triangle3 = crtTriangle(
    [1, 1, 0, 1],
    [-0.5,0,-2]
)

const triangle4 = crtTriangle(
    [1, 1, 0, 1],
    [0.5,0,-2]
)

function crtTriangle(color, [x,y,z]) {
    return new Poly({
        gl,
        source: [
            x, 0.3+y, z,
            -0.3+x, -0.3+y, z,
            0.3+x, -0.3+y, z,
        ],
        type: 'TRIANGLES',
        attributes: {
            a_Position: {
                size: 3,
                index: 0
            },
        },
        uniforms: {
            u_Color: {
                type: 'uniform4fv',
                value: color
            },
            u_ProjectionMatrix: {
                type: 'uniformMatrix4fv',
                value: camera.projectionMatrix.elements
            },
        }
    })
}

gl.clear(gl.COLOR_BUFFER_BIT);
render()

function render() {
    gl.clear(gl.COLOR_BUFFER_BIT);

    triangle1.init()
    triangle1.draw()
    
    triangle2.init()
    triangle2.draw()

    triangle3.init()
    triangle3.draw()

    triangle4.init()
    triangle4.draw()
}

效果图

结合投影矩阵、视图矩阵、模型矩阵

投影矩阵、视图矩阵、模型矩阵的结合方式：

1
最终的顶点坐标=投影矩阵*视图矩阵*模型矩阵*初始顶点坐标
投影视图矩阵

1.在顶点着色器里把投影矩阵变成投影视图矩阵。

1
2
3
4
5
6
7
<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    uniform mat4 u_PvMatrix;
    void main(){
      gl_Position = u_PvMatrix*a_Position;
    }
</script>

2.设置相机位置，并让其看向一点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const eye = new Vector3(0, 1, 1)
const target = new Vector3(0, 0, -2.5)
const up = new Vector3(0, 1, 0)

const [fov,aspect,near,far]=[
    45,
    canvas.width / canvas.height,
    1,
    20
]

const camera = new PerspectiveCamera(fov,aspect,near,far)
camera.position.copy(eye)
camera.lookAt(target)
camera.updateWorldMatrix(true)

3.计算投影视图矩阵，即让相机的投影矩阵乘以视图矩阵

1
2
3
4
5
const pvMatrix = new Matrix4()
pvMatrix.multiplyMatrices(
    camera.projectionMatrix,
    camera.matrixWorldInverse,
)

4.修改一下建立三角形方法里的uniform 变量

1
2
3
4
u_PvMatrix: {
    type: 'uniformMatrix4fv',
    value: pvMatrix.elements
},

此时效果如下
效果图

投影视图矩阵乘以模型矩阵

之前我们设置三角形位置的时候，是直接对顶点的原始数据进行的修改。

1
2
3
4
5
source: [
    x, 0.3 + y, z,
    -0.3 + x, -0.3 + y, z,
    0.3 + x, -0.3 + y, z,
],

其实，我是可以将位移数据写进模型矩阵里的，当然旋转和缩放数据也可以写进去，然后用模型矩阵乘以原始顶点，从而实现对模型的变换。

1.顶点着色器

1
2
3
4
5
6
attribute vec4 a_Position;
uniform mat4 u_PvMatrix;
uniform mat4 u_ModelMatrix;
void main(){
    gl_Position = u_PvMatrix*u_ModelMatrix*a_Position;
}

2.在crtTriangle()方法里，把三角形的数据源写死，在uniforms 里添加一个模型矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function crtTriangle(color, modelMatrix) {
    return new Poly({
        gl,
        modelMatrix,
        source: [
            0, 0.3, 0,
            -0.3, -0.3, 0,
            0.3, -0.3, 0,
        ],
        type: 'TRIANGLES',
        attributes: {
            a_Position: {
                size: 3,
                index: 0
            },
        },
        uniforms: {
            u_Color: {
                type: 'uniform4fv',
                value: color
            },
            u_PvMatrix: {
                type: 'uniformMatrix4fv',
                value: pvMatrix.elements
            },
            u_ModelMatrix: {
                type: 'uniformMatrix4fv',
                value: modelMatrix
            },
        }
    })
}

3.建立四个三角形
这里的矩阵是列主序的，所以比如第一个三角形就是x轴移动-0.5,z轴移动-3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
const triangle1 = crtTriangle(
    [1, 0, 0, 1],
    [
        1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, 0,
        -0.5, 0, -3, 1,
    ]
)

const triangle2 = crtTriangle(
    [1, 0, 0, 1],
    [
        1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, 0,
        0.5, 0, -3, 1,
    ]
)

const triangle3 = crtTriangle(
    [1, 1, 0, 1],
    [
        1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, 0,
        -0.5, 0, -2, 1,
    ]
)

const triangle4 = crtTriangle(
    [1, 1, 0, 1],
    [
        1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, 0,
        0.5, 0, -2, 1,
    ]
)

效果图

结语

本篇文章就到这里了，更多内容敬请期待，债见~

可视化学习 WebGL学习
上一篇:
【可视化学习】84-从入门到放弃WebGL(十六)
下一篇:
【SVG学习】02-SVG动画

    • blog of codesigner