微信小程序版本更新提示

前言

本篇文章继续跟着李伟老师学习 webgl，本篇文章的内容主要为基点变换与它的衍生内容

基点变换原理

就比如这样一张图片，求：让 img 基于其左上角点 P 点进行旋转和缩放的方法

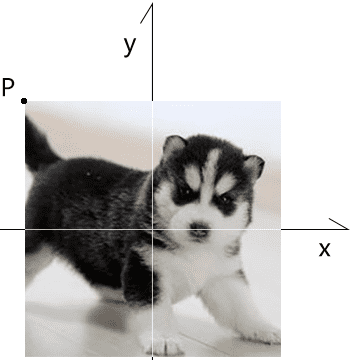
我们设置图片的本地矩阵为 mi,当前 mi 和世界坐标系重合。

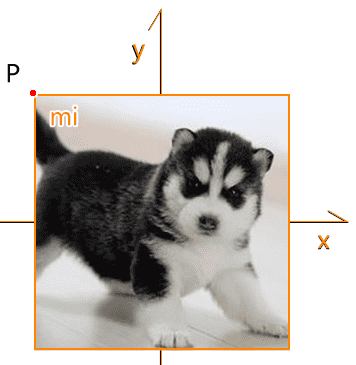
让 mi 的位置减去点 P

如果我们现在旋转 mi 的话，会基于 mi 的坐标原点旋转，这明显不是我们想要的。

新建本地矩阵 mb

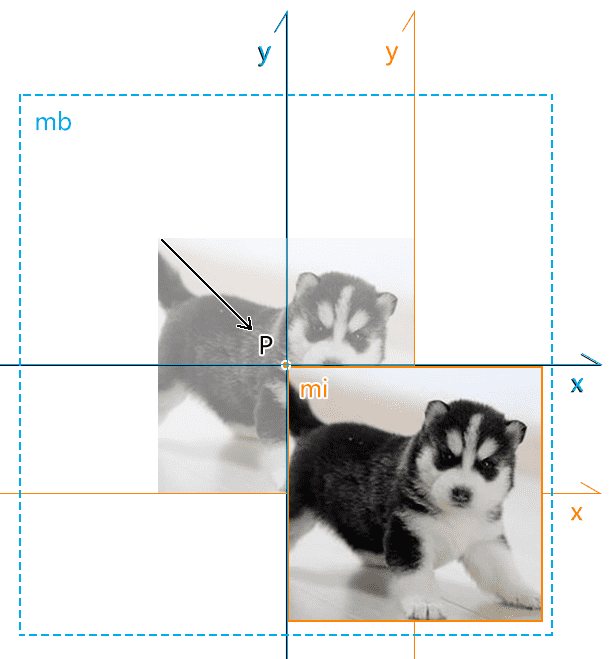
当前 mb 和世界坐标系重合。

然后让 mb 的位置加上点 P

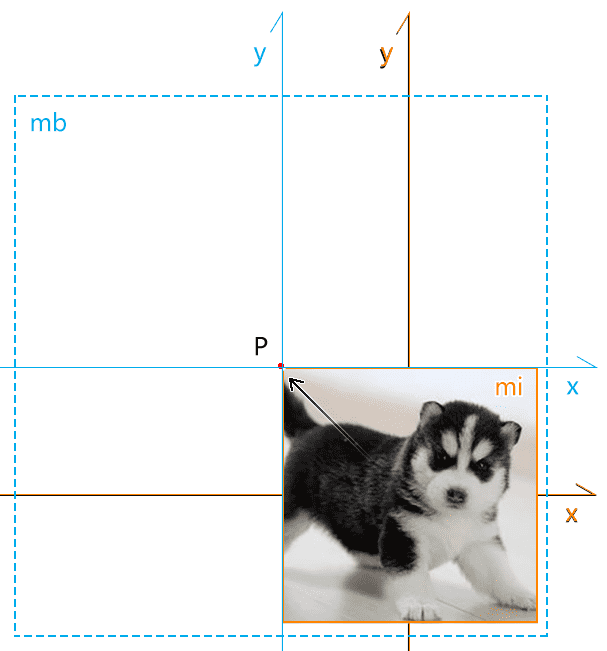
此时 mi 又和世界坐标系重合了
此时的 img 和最初始的 img 重合。
此时 img 的左上角点 P 和 mb 的坐标原点重合
此时我们旋转 mb，mi 会基于 mb 的坐标原点旋转，同时也带动了图片基于点 P 旋转。

计算模型矩阵，变换图片顶点的初始点位，从而得到图片顶点基于点 P 变换后的位置。
模型矩阵=mb*mi

图片顶点基于点 P 变换后的位置=模型矩阵*图片顶点的初始点位

mi 包含了图片的初始点位，可以理解为 three.js 中 Object3D。

mb 包含了 mi，可以理解为 three.js 中的 Group。

代码实现

着色器

这里的参数大家应该都比较熟了

• a_Position:顶点位置
• u_ModelMatrix:模型矩阵
• u_PvMatrix:视图矩阵
• v_Pin:通过顶点着色器传递给片元着色器的纹理(铆钉)
• a_Pin:纹理(铆钉)

<!-- 着纹理 -->
<script id="textureVertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  attribute vec2 a_Pin;
  uniform mat4 u_PvMatrix;
  uniform mat4 u_ModelMatrix;
  varying vec2 v_Pin;
  void main(){
    gl_Position = u_PvMatrix*u_ModelMatrix*a_Position;
    v_Pin=a_Pin;
  }
</script>
<script id="textureFragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  uniform sampler2D u_Sampler;
  varying vec2 v_Pin;
  void main(){
    gl_FragColor=texture2D(u_Sampler,v_Pin);
  }
</script>

导入

import { createProgram } from "../jsm/Utils.js";
import {
  Matrix4,
  OrthographicCamera,
  Vector3,
  Vector2,
} from "https://unpkg.com/three/build/three.module.js";
import OrbitControls from "./jsm/OrbitControls.js";
import Mat from "./jsm/Mat.js";
import Geo from "./jsm/Geo.js";
import Obj3D from "./jsm/Obj3D.js";
import Scene from "./jsm/Scene.js";

初始化 canvas 并设置正交相机

const canvas = document.getElementById("canvas");
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
const gl = canvas.getContext("webgl");
gl.clearColor(0.0, 0.0, 0.0, 1.0);

const halfH = 1;
const ratio = canvas.width / canvas.height;
const halfW = halfH * ratio;
const [left, right, top, bottom, near, far] = [
  -halfW,
  halfW,
  halfH,
  -halfH,
  1,
  8,
];
const eye = new Vector3(0, 0, 2);
const target = new Vector3(0, 0, 0);
const camera = new OrthographicCamera(left, right, top, bottom, near, far);
camera.position.copy(eye);
camera.lookAt(target);
camera.updateMatrixWorld();
const scence = new Scene({ gl });

投影视图矩阵

让相机的投影矩阵乘以视图矩阵

const pvMatrix = camera.projectionMatrix
  .clone()
  .multiply(camera.matrixWorldInverse);

定义顶点位置

/* 计算图片顶点 */
const [w, h] = [0.6, 0.6];
const [hw, hh] = [w / 2, h / 2];
// 左上角的点开始，三角带绘制逆时针--> 左上---左下---右上---右下
const vertices = new Float32Array([-hw, hh, -hw, -hh, hw, hh, hw, -hh]);

等待图片加载完成添加到场景中

这里用了前面文章封装的内容,这里的 a_Pin 你现在可以理解为固定的，因为它以左下角的点作为原点，因此按照三角带的绘制方式，左上角的点相当于(0,1),左下角的点相当于(0,0),右上角的点是(1,1),右下角的点是(1,0)

const image = new Image();
image.src = "./images/erha.jpg";
let mat = null;
image.onload = function () {
  const vs = document.getElementById("textureVertexShader").innerText;
  const fs = document.getElementById("textureFragmentShader").innerText;
  const program = createProgram(gl, vs, fs);
  mat = new Mat({
    program,
    data: {
      u_PvMatrix: {
        value: pvMatrix.elements,
        type: "uniformMatrix4fv",
      },
      u_ModelMatrix: {
        value: new Matrix4().elements,
        type: "uniformMatrix4fv",
      },
    },
    maps: {
      u_Sampler: {
        image,
      },
    },
    mode: "TRIANGLE_STRIP",
  });
  const geo = new Geo({
    data: {
      a_Position: {
        array: vertices,
        size: 2,
      },
      a_Pin: {
        array: new Float32Array([0, 1, 0, 0, 1, 1, 1, 0]),
        size: 2,
      },
    },
  });
  const obj = new Obj3D({ geo, mat });
  scence.add(obj);
  scence.draw();
};

声明本地矩阵

// 本地矩阵
const mi = new Matrix4();
// 本地矩阵
const mb = new Matrix4();
// 模型矩阵
const mm = new Matrix4();
// 基点
let orignInd = 0;

上面的模型矩阵 mm 之后会在渲染时，由 mb*mi 得到。

基于图片的变换基点布阵

这里的 orignInd 就是我们需要按照哪个点处理，比如是 0，那么得到的点位就是左上角的点，如果是 2，那么就是左下角的点，因为我们俩个点作为一个 xy 坐标， 依次类推，右上角的点就是 4，右下角就是 6,我们之前说过，mi 是减去 P 的本地矩阵，mb 是加上 P 的本地矩阵，所以 mi 设置为(-x,-y,0),mb 设置为(x,y,0)

setOrign(orignInd);
function setOrign(i) {
  const [x, y] = [vertices[i], vertices[i + 1]];
  mi.setPosition(-x, -y, 0);
  mb.setPosition(x, y, 0);
}

渲染变化

然后我们对模型矩阵进行沿 Z 轴旋转和 sin 函数缩放即可

let ang = 0;
function render() {
  ang += 0.02;
  const s = (Math.sin(ang) + 1) / 2;
  mm.copy(
    mb
      .clone()
      .multiply(new Matrix4().makeRotationZ(ang))
      .scale(new Vector3(s, s, 1))
      .multiply(mi)
  );
  mat.setData("u_ModelMatrix", {
    value: mm.elements,
  });
  scence.draw();
  requestAnimationFrame(render);
}

这里的基点变化其实就是利用了基变化的原理，这里给大家推荐个视频
https://www.bilibili.com/video/av6731067/?p=13

二次基点变换

假如我们需要每旋转 45 度就变换我们的基点，那么该如何实现呢，其实就是将 orignInd 加上 2，超过 6 就变成 0 即可，让他在 0,2,4,6 依次循环，然后为了让我们变化顺畅，我们需要加上 mm 的模型矩阵，在当前矩阵基础上进行变化，实现代码如下

function render() {
  ang += 0.005;
  if (ang > Math.PI / 4) {
    ang = 0;
    formatVertices();
    orignInd = (orignInd + 2) % 8;
    setOrign(orignInd);
  }
  const s = (Math.sin(ang * 8 + Math.PI / 2) + 1) / 2;
  mm.copy(
    mb
      .clone()
      .multiply(new Matrix4().makeRotationZ(ang))
      .scale(new Vector3(s, s, 1))
      .multiply(mi)
  );
  mat.setData("u_ModelMatrix", {
    value: mm.elements,
  });
  scence.draw();
  requestAnimationFrame(render);
}

function formatVertices() {
  for (let i = 0; i < vertices.length; i += 2) {
    const p = new Vector3(vertices[i], vertices[i + 1], 0).applyMatrix4(mm);
    vertices[i] = p.x;
    vertices[i + 1] = p.y;
  }
  geo.setData("a_Position", {
    array: vertices,
  });
}

用鼠标变换图片

功能描述

变换节点

变换节点就是图片的四个角点+描边。

变换节点没啥实际功能，就是整个视觉样式，让用户知道此图可变换。

位移

当鼠标在图片中的时候，按住鼠标可以拖拽图片。

缩放

当鼠标到图片节点的距离小于 15 像素时，开启鼠标对图片的缩放功能。

默认：居中+等比缩放

alt 键：以鼠标对面的点为基点进行缩放

shift 键：自由缩放

旋转

当鼠标到图片节点的距离小于 40 像素时，开启鼠标对图片的旋转功能。

默认：居中+按照特定弧度(15°)旋转

alt 键：以鼠标对面的点为基点进行旋转

shift 键：自由旋转

前期准备-图片+外框

准备俩套着色器

<!-- 点和线 -->
<script id="solidVertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  uniform mat4 u_PvMatrix;
  uniform mat4 u_ModelMatrix;
  void main(){
    gl_Position = u_PvMatrix*u_ModelMatrix*a_Position;
    gl_PointSize=10.0;
  }
</script>
<script id="solidFragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  void main(){
    gl_FragColor=vec4(1.0,1.0,1.0,1.0);
  }
</script>
<!-- 着纹理 -->
<script id="textureVertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  attribute vec2 a_Pin;
  uniform mat4 u_PvMatrix;
  uniform mat4 u_ModelMatrix;
  varying vec2 v_Pin;
  void main(){
    gl_Position = u_PvMatrix*u_ModelMatrix*a_Position;
    v_Pin=a_Pin;
  }
</script>
<script id="textureFragmentShader" type="x-shader/x-fragment">
  precision mediump float;
  uniform sampler2D u_Sampler;
  varying vec2 v_Pin;
  void main(){
    gl_FragColor=texture2D(u_Sampler,v_Pin);
  }
</script>

通过图片尺寸，获取图片和图片外框的顶点

// 图片尺寸
const [w, h] = [0.6, 0.6];
const [hw, hh] = [w / 2, h / 2];
// 图片顶点
const vertices = new Float32Array([-hw, hh, -hw, -hh, hw, hh, hw, -hh]);
// 图片外框顶点
let verticesOut = getVerticesOut();

/* 基于vertices获取verticesOut */
function getVerticesOut() {
  return new Float32Array([
    vertices[0],
    vertices[1],
    vertices[2],
    vertices[3],
    vertices[6],
    vertices[7],
    vertices[4],
    vertices[5],
  ]);
}

图片是用 TRIANGLE_STRIP 三角带画的；
图片外框是用 LINE_LOOP 闭合线条和点 POINTS 画的。
图片和图片外框的顶点排序是不同的。

绘制图片外框和图片

// 场景
const scence = new Scene({ gl });

// 图片外框-点和线
let matOut = null;
let geoOut = null;
{
  const vs = document.getElementById("solidVertexShader").innerText;
  const fs = document.getElementById("solidFragmentShader").innerText;
  const program = createProgram(gl, vs, fs);
  matOut = new Mat({
    program,
    data: {
      u_PvMatrix: {
        value: pvMatrix.elements,
        type: "uniformMatrix4fv",
      },
      u_ModelMatrix: {
        value: new Matrix4().elements,
        type: "uniformMatrix4fv",
      },
    },
    mode: ["LINE_LOOP", "POINTS"],
  });
  geoOut = new Geo({
    data: {
      a_Position: {
        array: verticesOut,
        size: 2,
      },
    },
  });
  const obj = new Obj3D({ geo: geoOut, mat: matOut });
  scence.add(obj);
}

// 图片
const image = new Image();
image.src = "./images/erha.jpg";
let mat = null;
let geo = null;
image.onload = function () {
  const vs = document.getElementById("textureVertexShader").innerText;
  const fs = document.getElementById("textureFragmentShader").innerText;
  const program = createProgram(gl, vs, fs);
  mat = new Mat({
    program,
    data: {
      u_PvMatrix: {
        value: pvMatrix.elements,
        type: "uniformMatrix4fv",
      },
      u_ModelMatrix: {
        value: new Matrix4().elements,
        type: "uniformMatrix4fv",
      },
    },
    maps: {
      u_Sampler: {
        image,
      },
    },
    mode: "TRIANGLE_STRIP",
  });
  geo = new Geo({
    data: {
      a_Position: {
        array: vertices,
        size: 2,
      },
      a_Pin: {
        array: new Float32Array([0, 1, 0, 0, 1, 1, 1, 0]),
        size: 2,
      },
    },
  });
  const obj = new Obj3D({ geo, mat });
  scence.unshift(obj);
  scence.draw();
};

scence.unshift(obj) 以前置的方式添加三维对象。

unshift(...objs) {
    const { children, gl } = this
    objs.forEach(obj => {
        children.unshift(obj)
        obj.parent=this
        obj.init(gl)
    })
}

之所以这么做是为了将图片放在图框下面，也就是先渲染图片，再渲染图框。

实现拖拽

声明一些必备变量

// 变换状态
let state = "none";
// 变换数据是否发生改变
let change = false;
// 变换状态与cursor状态的对应关系
const cursorMap = new Map([
  ["drag", "move"],
  ["rotate", "alias"],
  ["scale", "pointer"],
  ["none", "default"],
]);

// 拖拽起始位与结束位(世界坐标系)
const dragStart = new Vector2();
const dragEnd = new Vector2();
// 位移量
let offset = new Vector2();
// 本地矩阵
const mi = new Matrix4();
// 本地矩阵
const mb = new Matrix4();
// 模型矩阵
const mm = new Matrix4();

监听 canvas 的鼠标按下事件

canvas.addEventListener("mousedown", (event) => {
  // 获取鼠标的世界坐标位
  const mp = worldPos(event);
  // 获取变换状态，如果鼠标在图像里，那么变换状态就是'drag'
  if (isInImg(mp)) {
    state = "drag";
    dragStart.copy(mp);
  }
});

鼠标按下时，主要做了 2 件事情：

1. 鼠标在 canvas 中的位置转世界位，以便于判断鼠标和图片顶点的关系。

const mp = worldPos(event);
function worldPos({ clientX, clientY }) {
  const [hw, hh] = [canvas.width / 2, canvas.height / 2];
  // 裁剪空间位
  const cp = new Vector3((clientX - hw) / hw, -(clientY - hh) / hh, 0);
  // 鼠标在世界坐标系中的位置
  const p = cp.applyMatrix4(pvMatrix.clone().invert());
  return new Vector2(p.x, p.y);
}

回顾一下我们之前所学的矩阵知识：
裁剪空间位 = 投影视图矩阵 * 模型矩阵 * 初始顶点位
由上式可得：
初始顶点位=(投影视图矩阵*模型矩阵)的逆矩阵*裁剪空间位
因为图片顶点就是基于世界坐标系定位的，世界坐标系是单位矩阵，任何矩阵与单位矩阵相乘都不会发生改变，所以模型矩阵可以忽略。
最终，鼠标的世界点位就是这样的：

const p = cp.applyMatrix4(pvMatrix.clone().invert());

2. 获取变换状态，如果鼠标在图像里，那么变换状态就是’drag’。

if (isInImg(mp)) {
  state = "drag";
  dragStart.copy(mp);
}

isInImg(dragStart) 是判断鼠标是否在图像中的方法。

function isInImg(p) {
  return (
    inTriangle(p, [
      { x: vertices[0], y: vertices[1] },
      { x: vertices[2], y: vertices[3] },
      { x: vertices[4], y: vertices[5] },
    ]) ||
    inTriangle(p, [
      { x: vertices[4], y: vertices[5] },
      { x: vertices[2], y: vertices[3] },
      { x: vertices[6], y: vertices[7] },
    ])
  );
}

inTriangle()：判断顶点是否在三角形中，返回布尔值。

因为图片由两个三角形组成，所以我做了两次判断。

只要点位在任意三角形中，就说明点位在图片中。

至于判断点位是否在三角形中的方法，我们之前说过。

function inTriangle(p0, triangle) {
  let bool = true;
  for (let i = 0; i < 3; i++) {
    const j = (i + 1) % 3;
    const [p1, p2] = [triangle[i], triangle[j]];
    if (cross([p0, p1, p2]) < 0) {
      bool = false;
      break;
    }
  }
  return bool;
}
function cross([p0, p1, p2]) {
  const [ax, ay, bx, by] = [p1.x - p0.x, p1.y - p0.y, p2.x - p0.x, p2.y - p0.y];
  return ax * by - bx * ay;
}

监听 canvas 的鼠标移动事件

canvas.addEventListener("mousemove", (event) => {
  // 获取鼠标世界位
  const mp = worldPos(event);
  // 设置鼠标样式
  if (state === "none") {
    let cursorState = "none";
    if (isInImg(mp)) {
      cursorState = "drag";
    }
    canvas.style.cursor = cursorMap.get(cursorState);
    return;
  }
  // 变换图片
  dragEnd.copy(mp);
  change = true;
  switch (state) {
    case "drag":
      drag();
      break;
  }
  //渲染
  render();
});

鼠标移动时，主要做了 4 件事情：

获取鼠标世界位，以便于判断鼠标和图片顶点的关系。

设置鼠标样式，此操作是在图片不处于任何变换状态时执行的。

变换图片

drag()：通过拖拽结束位减拖拽起始位得到图片的偏移量。

function drag() {
  offset.copy(dragEnd.clone().sub(dragStart));
}

渲染 render()

function render() {
  const { elements } = mm.copy(getModelMatrix());
  mat.setData("u_ModelMatrix", {
    value: elements,
  });
  matOut.setData("u_ModelMatrix", {
    value: elements,
  });
  scence.draw();
}

计算模型矩阵的方法 getModelMatrix()

function getModelMatrix() {
  // 位移矩阵
  const { x: px, y: py } = offset;
  const moveMatrix = new Matrix4().set(
    1,
    0,
    0,
    px,
    0,
    1,
    0,
    py,
    0,
    0,
    1,
    0,
    0,
    0,
    0,
    1
  );
  // 模型矩阵
  return mb.clone().multiply(moveMatrix).multiply(mi);
}

监听 canvas 的鼠标抬起事件

canvas.addEventListener("mouseup", () => {
  if (state !== "none") {
    state = "none";
    if (change) {
      change = false;
      offset.set(0, 0);
      canvas.style.cursor = "default";
      formatVertices();
    }
  }
});

鼠标抬起时，主要做了以下事情：

• 清理 state 状态
• 清空图片的变换数据
• 恢复鼠标样式
• 格式化顶点数据，并更新几何体的顶点集合

function formatVertices() {
  for (let i = 0; i < vertices.length; i += 2) {
    const p = new Vector3(vertices[i], vertices[i + 1], 0).applyMatrix4(mm);
    vertices[i] = p.x;
    vertices[i + 1] = p.y;
  }
  verticesOut = getVerticesOut();
  geo.setData("a_Position", {
    array: vertices,
  });
  geoOut.setData("a_Position", {
    array: verticesOut,
  });
}

实现旋转

声明必备变量

// 变换基点
let orign = new Vector2();
// 拖拽起始位与结束位减变换基点位
const start2Orign = new Vector2();
const end2Orign = new Vector2();
// 旋转起始弧度
let startAng = 0;
// 旋转量
let angle = 0;

鼠标按下

canvas.addEventListener("mousedown", (event) => {
  // 获取鼠标拖拽的起始位dragStart，此位置为世界坐标位
  const mp = worldPos(event);
  // 获取变换状态，如果鼠标在图像里，那么变换状态就是'drag'
  if (isInImg(mp)) {
    state = "drag";
    dragStart.copy(mp);
  } else {
    const node = selectNode(mp);
    if (node) {
      dragStart.copy(mp);
      state = node.state;
      setOrign();
      start2Orign.subVectors(dragStart, orign);
      startAng = Math.atan2(start2Orign.y, start2Orign.x);
    }
  }
});

鼠标按下时，只要不是在图片里，就会做以下事情：

选择节点 selectNode(dragStart)，返回节点索引和变换状态

function selectNode(m) {
  let node = null;
  for (let i = 0; i < vertices.length; i += 2) {
    const v = new Vector2(vertices[i], vertices[i + 1]);
    const len = (m.clone().sub(v).length() * canvas.height) / 2;
    if (len < 40) {
      node = { index: i, state: "rotate" };
      break;
    }
  }
  return node;
}

若选中节点，则更新变换状态、基点、拖拽起点相对于基点的位置、起始弧度。

详细看一下设置基点的方法：

function setOrign() {
  const { x, y } = getCenter();
  orign.set(x, y);
  mi.makeTranslation(-x, -y, 0);
  mb.makeTranslation(x, y, 0);
}
function getCenter() {
  let [x1, y1] = [vertices[0], vertices[1]];
  let [x2, y2] = [vertices[6], vertices[7]];
  return new Vector2(x1 + (x2 - x1) / 2, y1 + (y2 - y1) / 2);
}

鼠标移动

canvas.addEventListener('mousemove', event => {
    // 获取鼠标世界位
    const mp = worldPos(event)
    // 设置鼠标样式
    if (state === 'none') {
        let cursorState = 'none'
        if (isInImg(mp)) {
            cursorState = 'drag'
        } else {
            const node = selectNode(mp)
            cursorState = node ? node.state : 'none'
        }
        canvas.style.cursor = cursorMap.get(cursorState)
        return
    }
    // 变换图片
    dragEnd.copy(mp)
    end2Orign.subVectors(mp, orign)
    change = true
    switch (state) {
        case 'drag':
            drag()
            break
        case 'rotate':
            rotate()
            break
    }
    //渲染
    render()
})

rotate() 旋转方法

function rotate() {
    const endAng = Math.atan2(end2Orign.y, end2Orign.x)
    angle = endAng - startAng
}

render() 方法无需改变，只是其中获取模型矩阵getModelMatrix() 的方法里，需要把旋转量算进去。

function getModelMatrix() {
    // 位移矩阵
    const { x: px, y: py } = offset
    const moveMatrix = new Matrix4().set(
        1, 0, 0, px,
        0, 1, 0, py,
        0, 0, 1, 0,
        0, 0, 0, 1,
    )
    // 旋转矩阵
    const [s, c] = [Math.sin(angle), Math.cos(angle),]
    const rotateMatrix = new Matrix4().set(
        c, -s, 0, 0,
        s, c, 0, 0,
        0, 0, 1, 0,
        0, 0, 0, 1,
    )
    // 模型矩阵
    return mb.clone()
        .multiply(moveMatrix)
        .multiply(rotateMatrix)
        .multiply(mi)
}

鼠标抬起

canvas.addEventListener('mouseup', () => {
    if (state !== 'none') {
        state = 'none'
        if (change) {
            change = false
            offset.set(0, 0)
            angle = 0
            canvas.style.cursor = 'default'
            formatVertices()
        }
    }
})

图片旋转的整体逻辑就是这样，当前图片默认是基于图片中心自由旋转。

我们可以再为其做一下优化：按住alt键，基于鼠标对面的节点变换。

alt 键改变基点

// 当前按下的键
let keys = new Set()
// 当前节点索引
let nodeInd = 0
// 节点对面的点
const opposite = new Map([[0, 6], [2, 4], [6, 0], [4, 2]])

// 监听canvas的鼠标按下事件
canvas.addEventListener('mousedown', event => {
    // 获取鼠标拖拽的起始位dragStart，此位置为世界坐标位
    const mp = worldPos(event)
    // 获取变换状态，如果鼠标在图像里，那么变换状态就是'drag'
    if (isInImg(mp)) {
        state = 'drag'
        dragStart.copy(mp)
    } else {
        const node = selectNode(mp)
        if (node) {
            dragStart.copy(mp)
            state = node.state
            nodeInd = node.index
            setOrign()
            start2Orign.subVectors(dragStart, orign)
            startAng = Math.atan2(start2Orign.y, start2Orign.x)
        }
    }
})

window.addEventListener('keydown', ({ keyCode }) => {
    keys.add(keyCode)
    setOrign()
})
window.addEventListener('keyup', ({ keyCode }) => {
    keys.delete(keyCode)
    setOrign()
})

/* 设置基点 */
function setOrign() {
    const { x, y } = keys.has(18) ? getOppo() : getCenter()
    orign.set(x, y)
    mi.makeTranslation(-x, -y, 0)
    mb.makeTranslation(x, y, 0)
}

// 对面的点
function getOppo() {
    const i2 = opposite.get(nodeInd)
    return new Vector2(vertices[i2], vertices[i2 + 1])
}
// 中点
function getCenter() {
    let [x1, y1] = [vertices[0], vertices[1]]
    let [x2, y2] = [vertices[6], vertices[7]]
    return new Vector2(
        x1 + (x2 - x1) / 2,
        y1 + (y2 - y1) / 2
    )
}

默认按照特定弧度旋转。按住shift键时，再自由旋转。

// 每次旋转的弧度
let angSpace = Math.PI / 12
function rotate() {
    const endAng = Math.atan2(end2Orign.y, end2Orign.x)
    angle = endAng - startAng
    if (!keys.has(16)) {
        angle = Math.round(angle / angSpace) * angSpace
    }
}

实现缩放

建立必备变量

// 缩放量
let zoom = new Vector2(1, 1)

鼠标移动

canvas.addEventListener('mousemove', event => {
    ……
    switch (state) {
            ……
            case 'scale':
                scale()
                break
    }
    render()
})

/* 缩放 */
function scale() {
    const sx = end2Orign.x / start2Orign.x
    const sy = end2Orign.y / start2Orign.y
    if (keys.has(16)) {
        //自由缩放
        zoom.set(sx, sy)
    } else {
        //等比缩放
        const ratio = end2Orign.length() / start2Orign.length()
        zoom.set(
            ratio * sx / Math.abs(sx),
            ratio * sy / Math.abs(sy),
        )
    }
}

选择节点

function selectNode(m) {
    let node = null
    for (let i = 0; i < vertices.length; i += 2) {
        const v = new Vector2(vertices[i], vertices[i + 1])
        const len = m.clone().sub(v).length() * canvas.height / 2
        if (len < 15) {
            node = { index: i, state: 'scale' }
            break
        } else if (len < 40) {
            node = { index: i, state: 'rotate' }
            break
        }
    }
    return node
}

鼠标抬起

canvas.addEventListener('mouseup', event => {
    ……
    zoom = new Vector2(1, 1)
    ……
})

模型矩阵

function getModelMatrix() {
    // 位移矩阵
    const { x: px, y: py } = offset
    const moveMatrix = new Matrix4().set(
        1, 0, 0, px,
        0, 1, 0, py,
        0, 0, 1, 0,
        0, 0, 0, 1,
    )
    // 旋转矩阵
    const [s, c] = [Math.sin(angle), Math.cos(angle),]
    const rotateMatrix = new Matrix4().set(
        c, -s, 0, 0,
        s, c, 0, 0,
        0, 0, 1, 0,
        0, 0, 0, 1,
    )
    // 缩放矩阵
    const { x: sx, y: sy } = zoom
    const scaleMatrix = new Matrix4().set(
        sx, 0, 0, 0,
        0, sy, 0, 0,
        0, 0, 1, 0,
        0, 0, 0, 1,
    )
    // 模型矩阵
    return mb.clone()
        .multiply(moveMatrix)
        .multiply(rotateMatrix)
        .multiply(scaleMatrix)
        .multiply(mi)
}

其实我们也可以使用Matrix4 对象内置的方法进行变换。

function getModelMatrix() {
    return mb.clone()
        .multiply(
            new Matrix4().makeTranslation(
                position.x, position.y, 0
            )
        )
        .multiply(
            new Matrix4().makeRotationZ(angle)
        )
        .scale(new Vector3(zoom.x, zoom.y, 1))
        .multiply(mi)
}

到目前为止，缩放的基本流程就搞定了。

然而，镜像缩放时，还会带来一个坑，此坑会影响图片的选择。

我们之前是通过下面的方法判断点位是否在三角形中的：

function inTriangle(p0, triangle) {
  let bool = true;
  for (let i = 0; i < 3; i++) {
    const j = (i + 1) % 3;
    const [p1, p2] = [triangle[i], triangle[j]];
    if (cross([p0, p1, p2]) < 0) {
      bool = false;
      break
    }
  }
  return bool;
}
function cross([p0, p1, p2]) {
  const [ax, ay, bx, by] = [
    p1.x - p0.x,
    p1.y - p0.y,
    p2.x - p0.x,
    p2.y - p0.y,
  ];
  return ax * by - bx * ay;
}

上面的 cross([p0, p1, p2]) < 0 是针对逆时针绘图的情况来判断的。

若是顺时针绘图，点位在三角形中需要满足的条件就应该是cross([p0, p1, p2]) > 0

因此我们需要判断一下，这个图片是逆时针画的，还是顺时针画的。

之前我们说过一个原理：叉乘是有方向的。

通过上面的原理可以知道：在二维多边形中，通过叉乘求出的多边形的面积是有正负之分的。

通过这个多边形的面积的正负，便可以判断图片是逆时针画的，还是顺时针画的。

接下来咱们通过代码说一下其具体实现过程。

先封装一个按逆时针获取图片中两个三角形的方法，以便复用

function getTriangles() {
    return [
        [
            { x: vertices[0], y: vertices[1] },
            { x: vertices[2], y: vertices[3] },
            { x: vertices[4], y: vertices[5] },
        ],
        [
            { x: vertices[4], y: vertices[5] },
            { x: vertices[2], y: vertices[3] },
            { x: vertices[6], y: vertices[7] },
        ]
    ]
}

再封装一个获取面积的方法

function getArea() {
    const [t1, t2] = getTriangles()
    return cross(t1) + cross(t2)
}

上面所求的面积实际上是图片面积的两倍，不过这都无所谓，我只需要面积的正负。

声明面积变量

// 面积
let area = getArea()

在判断点位是否在三角形中的时候，乘上面积

function inTriangle(p0, triangle) {
    let bool = true;
    for (let i = 0; i < 3; i++) {
        const j = (i + 1) % 3;
        const [p1, p2] = [triangle[i], triangle[j]];
        if (area * cross([p0, p1, p2]) < 0) {
            bool = false;
            break
        }
    }
    return bool;
}

面积需要随顶点数据的格式化同步更新

function formatVertices() {
    for (let i = 0; i < vertices.length; i += 2) {
        const p = new Vector3(vertices[i], vertices[i + 1], 0)
        .applyMatrix4(mm)
        vertices[i] = p.x
        vertices[i + 1] = p.y
    }
    area = getArea()
    geo.setData('a_Position', {
        array: vertices
    })
    geoOut.setData('a_Position', {
        array: getVerticesOut()
    })
}

保留初始点位

我之前在变换图片时，其实还有一处瑕疵，那就是无法保留初始点位。

初始点位与浮点数进行多次运算，容易引起数据失真。

当然，若变换次数不多，肉眼是很难发现失真的。

对于上面的问题，我们是可以通过保留初始点位来解决的。

接下来咱们说一下其实现思路。

实现思路

已知：图片img

求：基于图片的左上角点P变换图片，且保留图片初始点位的方法

解：

搭建矩阵

把图片装画框里，画框的本地矩阵是mh
把画框装盒子里，盒子的本地矩阵是mi
把盒子装抽屉里，抽屉的本地矩阵是mb

设置变换基点：

mi-P
mb+P

变换抽屉的本地矩阵mb

在第二次变换时，将所有变换数据合入画框mh中

渲染时的模型矩阵：

mb*mi*mh

代码实现

在之前代码的基础上进行修改。

声明必备数据

// 图片初始顶点
const verticesBasic = new Float32Array([
    -hw, hh,
    -hw, -hh,
    hw, hh,
    hw, -hh,
])
// 图片顶点的世界位
const vertices = Float32Array.from(verticesBasic)
// 画框本地矩阵
const mh = new Matrix4()

将图片和图片外框的顶点数据写死，之后在变换的时候无需修改初始点位，直接修改模型矩阵即可。

geoOut = new Geo({
    data: {
        a_Position: {
            array: new Float32Array([
                verticesBasic[0], verticesBasic[1],
                verticesBasic[2], verticesBasic[3],
                verticesBasic[6], verticesBasic[7],
                verticesBasic[4], verticesBasic[5],
            ]),
            size: 2
        },
    }
})
……
geo = new Geo({
    data: {
        a_Position: {
            array: verticesBasic,
            size: 2
        },
        a_Pin: {
            array: new Float32Array([0, 1,0, 0,1, 1,1, 0,]),
            size: 2
        }
    }
})

在格式化顶点数据的方法里，已经无需更新几何体的顶点数据，只需要获取图片顶点的世界位即可。

function formatVertices() {
    mh.copy(mm.clone().multiply(mh))
    for (let i = 0; i < verticesBasic.length; i += 2) {
        const p = new Vector3(verticesBasic[i], verticesBasic[i + 1], 0)
        .applyMatrix4(mh)
        vertices[i] = p.x
        vertices[i + 1] = p.y
    }
    area = getArea()
}

在渲染方法里计算模型矩阵的时候，再乘上画框的本地矩阵

function render() {
    mm.copy(getModelMatrix())
    const { elements } = mm.clone().multiply(mh)
    mat.setData('u_ModelMatrix', {
        value: elements
    })
    matOut.setData('u_ModelMatrix', {
        value: elements
    })
    scence.draw()
}

关于鼠标对图像的变换我们就说到这。

虽然我们在这里是拿二维图片举的例子，然而其实现思想都是按三维走的，就比如模型矩阵的运算。

通过上面的例子，大家可以知道修改模型的两种方式：

1. 直接修改构成模型的初始点位
2. 修改模型矩阵

当然，上面的操作最终都是在移动模型的初始点位，只是其应用场景会有所不同。

前者适合对模型的局部顶点进行修改，就比如对图片的某一个顶点进行拉扯。

后者适合对模型的所有顶点统一变换。

大家理解了这两种方式的差异，也就知道了在three.js 里什么时候要修改BufferGeometry对象里的顶点，什么时候修改Object3D对象的本地矩阵。

结语

本篇文章就到这里了，更多内容敬请期待，债见~